《湖泊科学》

长江中游急弯段二维水沙数学模型及应用^*

doi: 10.18307/2025.0343

刘鑫^1,2 ，夏军强¹ ，邓珊珊¹ ，周美蓉¹

1. 武汉大学，水资源工程与调度全国重点实验室，武汉 430072

2. 长江水利委员会水文局，武汉 430010

基金项目: 国家自然科学基金项目（U2040215,52479075）；国家重点研发计划项目（2023YFC3209504）联合资助

Two-dimensional morphodynamic model and its application in the sharp bend of the middle Yangtze River^*

Liu Xin^1,2 ， Xia Junqiang¹ ， Deng Shanshan¹ ， Zhou Meirong¹

1. State Key Laboratory of Water Resources Engineering and Management, Wuhan University, Wuhan 430072 , P.R.China

2. Bureau of Hydrology, Changjiang Water Resources Commission of the Ministry of Water Resources, Wuhan 430010 , P.R.China

摘要

深入研究急弯段水沙输移及河床变形的数值模拟方法，能为长江中游河段河势预测提供技术支撑，具有重要意义。本文在基于单元中心格式有限体积法的二维水沙数学模型基础上，考虑整治工程和二次流的影响，构建了适用于急弯段的二维水沙数学模型。将改进后的模型应用于长江中游监利-城陵矶河段。本研究主要结论如下：（ⅰ）考虑整治工程影响时对计算河段中有工程的区域进行节点代码标记，计算过程中有整治工程且前期模拟未形成可冲层的区域不发生冲刷，考虑二次流修正时计算了扩散应力项，用于反映二次流对垂线平均流速横向分布的影响；（ⅱ）采用2014年和2018年监利-城陵矶河段的实测水沙及地形资料对模型进行率定及验证，计算结果表明：广兴洲站水位过程的纳什效率系数在0.97以上，且急弯段典型断面水深、垂线平均流速及含沙量横向分布的计算值与实测值符合较好，故改进后的模型可以较准确地模拟急弯段水沙输移过程；(ⅲ) 下荆江急弯段弯顶上游的主流线偏靠凸岸，在弯顶下游才向凹岸摆动，比已有研究报道的急弯段的主流摆动过程更滞后，且观音洲弯道凹岸弯顶上游和凸岸弯顶下游均存在回流区。七弓岭和观音洲弯道含沙量均呈现凸岸高于凹岸的特点，且河床总体呈现凸冲凹淤的特点。

关键词

二维水沙模型 / 整治工程 / 二次流 / 急弯段 / 长江中游

Abstract

It is of great significance to establish a numerical model of flow-sediment transport and riverbed deformation in the sharp bends to provide technical support for the prediction of river regime in the middle Yangtze River (MYR). A two-dimensional model based on the finite volume method of element center format was established to simulate the flow-sediment transport and riverbed deformation processes in the sharp bends, considering the effects of river regulation projects and secondary flow. The improved model was applied to the Jianli-Chenglingji sub-reach of the MYR. The results indicated that: (ⅰ) when considering the influence of regulation projects, the nodes were marked with codes for the area protected by revetment works, which cannot be scoured in the calculation, and the diffusion stress term was calculated to consider the effect of secondary flow on the transverse distribution of depth-averaged flow velocity; (ⅱ) the model was calibrated and verified based on the measurements of flow, sediment and topographic data of the Jianli-Chenglingji reach in 2014 and 2018, respectively, and the results indicated that the NSEs of section-averaged water level at Guangxingzhou were more than 0.97, and other hydrological parameters of depth, depth-averaged flow velocity and sediment concentration at several cross-sections were in agreement with the measured data. Therefore, the improved model can accurately simulate the flow-sediment transport process in the sharp bend; (ⅲ) the mainstream line was located near the inner bank upstream of the bend apex, and shifted towards the outer bank downstream of the bend apex in the sharp bends of Qigongling (QGL) and Guanyinzhou (GYZ), which was more delayed than the shift process of mainstream line in the sharp bends reported in previous studies. Flow recirculation zones can be observed near the outer bank upstream of the bend apex and near the inner bank downstream of the bend apex of GYZ bend. The depth-averaged sediment concentration near the inner bank was higher than outer bank in the QGL and GYZ bends, and the riverbed deformation was characterized by erosion of inner bank and deposition of outer bank.

Keywords

Two-dimensional morphodynamic model / regulation works / secondary flow / sharp bend / middle Yangtze River

1 急弯河段二维水沙数学模型 1.1 控制方程与数值解法 1.1.1 控制方程 1.1.2 数值解法 1.2 考虑整治工程影响的模块 1.2.1 河床边界条件的设定 1.2.2 输沙及河床冲淤计算的改进 1.3 考虑二次流影响的模块 1.4 改进后模型的计算步骤 2 长江中游典型急弯段水沙输移及河床冲淤过程模拟 2.1 河段概况 2.2 模型计算条件 2.2.1 进出口边界条件 2.2.2 河床边界条件 2.2.3 动边界处理及模型参数设置 2.3 典型断面的模拟结果 2.3.1 水位过程的率定与验证结果 2.3.2 水深、垂线平均流速和含沙量的率定与验证结果 2.4 急弯段特定流量下的流速和含沙量分布 2.4.1 垂线平均流速的横向分布 2.4.2 垂线平均含沙量的横向分布 2.4.3 急弯段河床冲淤分布 3 结论

弯曲河流是天然河流中分布最广的河型，其水流结构特点及河床演变规律受到学术界和工程界的广泛关注^[1-2]。弯道通常由微弯演变成急弯，然后发生切滩、撇弯或裁弯等现象，故急弯段的河床更不稳定^[3]。因此，在掌握急弯段演变机理的基础上，深入研究其水沙输移及河床变形模拟方法，可为河势预测提供技术支撑，具有重要意义。

针对急弯河段的数学模型通常包括弯道平面形态及迁移过程的模拟、弯道水沙动力的模拟以及河床形态的模拟^[4]。这三者相互联系，如平面形态及迁移过程的模拟依赖于河床形态调整模拟，而河床形态调整模拟又依赖于水沙动力的计算。夏军强和王光谦^[5]在正交曲线坐标系的平面二维水沙动力学模型中考虑了粘性河岸的冲刷崩退过程，实现了对游荡型和弯曲型河段水沙输移及河床变形的模拟。Deng等^[6]将平面二维水沙数学模块和二元结构河岸崩退模块结合，模拟了荆江河段的水流运动、床面冲淤及河岸崩退过程。Crosato^[7]在平面二维水沙及河床冲淤数学模型的基础上，耦合了河岸侵蚀模块、河岸淤进模块以及裁弯模块，构建了弯曲河道的演变模型。Duan和Julien^[8]在基于结构化网格的二维水沙模型中，结合动网格技术考虑了河岸崩退过程，模拟了室内水槽中顺直段形成弯曲段，并由微弯演变成急弯的过程。Turnipseed等^[9]采用MIKE 21二维动网格水流模型模拟了急弯段裁弯过程中不同阶段的流速分布，发现颈口存在多个回流结构。上述模型主要考虑了弯曲段的河岸变形过程，而长江中游急弯段两岸均逐步实施了护岸工程，河床形态调整主要体现为床面冲淤的横向分布。急弯段河床冲淤分布与二次流密切相关，故有必要在模型中充分考虑整治工程和二次流的影响。除模型功能的拓展外，部分学者提出采用局部时间步长技术提高模型的计算效率，并将模型应用于长江典型分汊段水沙输移及河床变形的模拟^[10-12]。此外，Olsen^[13]采用三维模型计算了弯曲段的水流运动，并利用动网格技术模拟了河岸的运动。假冬冬等^[14]耦合三维水沙输移模块与崩岸模块，模拟了石首弯道段的崩岸过程。三维模型可以更精准地模拟弯曲河段的复杂水沙运动，但受限于计算效率，只能模拟局部河段短时间尺度的水沙输移及河床冲淤过程，难以适用于长河段、长时间尺度的水沙输移及冲淤过程模拟。

本文在已有基于单元中心格式有限体积法的二维水沙动力学模型的基础上，增加考虑整治工程和二次流影响的模块，构建适用于急弯段的二维水沙数学模型，并采用OpenMP并行技术提高模型的计算效率。将改进后的模型应用到长江中游监利-城陵矶河段，模拟并分析了七弓岭和观音洲两个典型急弯段的水沙输移及河床冲淤过程。

1 急弯河段二维水沙数学模型

1.1 控制方程与数值解法

1.1.1 控制方程

本文采用的二维水沙控制方程由浑水连续方程、运动方程、泥沙输移方程和河床变形方程组成。由于长江中下游含沙量较低且河床变形速率慢，忽略水沙耦合项时，控制方程组的守恒形式可表示为：

\frac{\partial U}{\partial t} + \frac{\partial E (U)}{\partial x} + \frac{\partial G (U)}{\partial y} = \frac{\partial \tilde{E} (U)}{\partial x} + \frac{\partial \tilde{G} (U)}{\partial y} + S

(1)

\frac{Δ Z_{s k}}{Δ t} = \frac{α_{s k}}{ρ^{'}} ω_{s k} (S_{k} - S_{* k})

(2)

式中，U为守恒变量向量；E和G分别为x和y方向的对流通量向量；

\tilde{E}

和

\tilde{G}

为扩散向量；S为源项向量。ΔZ_sk为第k组泥沙输移引起的河床变形厚度；α_sk和ω_sk分别为第k组泥沙的恢复饱和系数和浑水中的沉速；ρ′为床沙干密度；S_k和S_*_k分别为第k组泥沙的含沙量和水流挟沙力。其中U、E、G、

\tilde{E}

、

\tilde{G}

、S的表达式如下：

U = [\begin{matrix} h \\ h u \\ h v \\ h S_{k} \end{matrix}]

(3)

E = [\begin{matrix} h u \\ h u^{2} + \frac{1}{2} g h^{2} \\ h u v \\ h u S_{k} \end{matrix}]

(4)

G = [\begin{matrix} h v \\ h u v \\ h v^{2} + \frac{1}{2} g h^{2} \\ h v S_{k} \end{matrix}]

(5)

\tilde{E} = [\begin{matrix} 0 \\ h (T_{x x} + D_{x x}) \\ h (T_{y x} + D_{y x}) \\ ε S_{k x} \end{matrix}]

(6)

\tilde{G} = [\begin{matrix} 0 \\ h (T_{x y} + D_{x y}) \\ h (T_{y y} + D_{y y}) \\ ε S_{k y} \end{matrix}]

(7)

S = S_{b} + S_{r} = [\begin{matrix} 0 \\ g h S_{b x} \\ g h S_{b y} \\ 0 \end{matrix}] + [\begin{matrix} 0 \\ - g h S_{f x} \\ - g h S_{f y} \\ - α_{s k k} ω_{s k} (S_{k} - S_{* k}) \end{matrix}]

(8)

式中，h为水深，u和v分别为x和y方向的流速；S_b和S_r分别为底坡源项和除底坡之外的源项；S_b_x和S_b_y分别为x和y方向的河床比降，

S_{b x} = - \partial Z_{b} / \partial x ， S_{b y} = - \partial Z_{b} / \partial y

，其中Z_b为床面高程；S_f_x和S_f_y分别为x和y方向的摩阻坡度，可表示为

S_{f x} = n^{2} u \sqrt{u^{2} + v^{2}} / h^{4 / 3} ， S_{f y} = n^{2} v \sqrt{u^{2} + v^{2}} / h^{4 / 3}

，其中n为曼宁糙率系数；T_xx、T_xy、T_yx、T_yy为水深平均的雷诺应力项；D_xx、D_xy、D_yx、D_yy为扩散应力项；ε为泥沙扩散系数；

S_{k x} = \partial S_{k} / \partial x ， S_{k y} = \partial S_{k} / \partial y

；雷诺应力项和扩散应力项的表达式为^[15]：

T_{x x} = 2 ν_{t} (\partial u / \partial x)

(9)

T_{x y} = T_{y x} = ν_{t} (\partial u / \partial y + \partial v / \partial x)

(10)

T_{y y} = 2 ν_{t} (\partial v / \partial y)

(11)

D_{x x} = \frac{1}{h} \int_{0}^{h} (u (z) - u)^{2} d z

(12)

D_{y y} = \frac{1}{h} \int_{0}^{h} (v (z) - v)^{2} d z

(13)

式中，ν_t为紊动粘滞系数；u（z）为u沿垂线的分布；v（z）为v沿垂线的分布。

1.1.2 数值解法

本文采用有限体积法求解二维水沙控制方程，将计算区域划分为无结构三角网格，守恒变量值储存在网格中心，相邻网格单元通过界面连接。采用HLL格式计算界面通量，其中黎曼问题中波速的计算参考Fraccarollo 和Toro^[16]提出的方法。采用Duran等^[17]提出的基于MUSCL格式改进的变量重构方法确保空间的二阶精度，该方法将浅水控制方程中的水深替换为水位，其数值离散格式严格满足well-balance特性和水深正性，本文模型仍以水深为守恒变量，主要借鉴其通量计算方法。底坡源项采用Valiani和Begnudelli^[18]提出的DFB方法进行离散求解，摩阻项则采用半隐式模式计算。采用预估、校正两步格式确保时间的二阶精度^[19]。此外，采用OpenMP并行技术提高模型的计算效率。

1.2 考虑整治工程影响的模块

下荆江急弯段实施了大量河道及航道整治工程，有必要考虑其对流速、含沙量及河床冲淤分布的影响，故本文在模型中增加了考虑整治工程影响的模块。此处介绍河床边界条件的设定和输沙及河床冲淤模块的改进。

1.2.1 河床边界条件的设定

根据长程河道地形中的高程数据及整治工程的分布情况，将河道划分为主槽、滩地、边（心）滩和整治工程4类区域，并给网格节点赋予特定的编号（TN=0，1，2，3）。将平均枯水位以下的区域标记为主槽（TN=0）；平滩高程以上区域标记为滩地（TN=1）；枯水位至平滩高程区域标记为边（心）滩（TN=2）；实施整治工程的区域均标记为TN=3（图1）。由于变量储存在单元中心，需确定单元属性，本文将单元编号取为三角形网格3个节点编号的最大值。

在生成网格之前，根据长程河道地形图中的整治工程分布情况，绘制出工程的位置及轮廓。长江中游弯曲段实施的整治工程类型主要为护岸和护滩工程，丁坝等挑流工程较少，故本文主要考虑护岸和护滩工程。长程河道地形图中护滩工程给出了明确的位置及形状，而护岸工程只能确定其长度，无法确定其横向宽度。考虑到弯曲段护岸工程通常实施在深泓贴岸的迎流顶冲段，故此处近似认为岸顶至坡脚均被工程守护。对于丁坝等挑流工程可设置成矩形固壁边界。在确定了各守护工程的边界后，生成无结构网格，并对主槽区域进行局部加密。

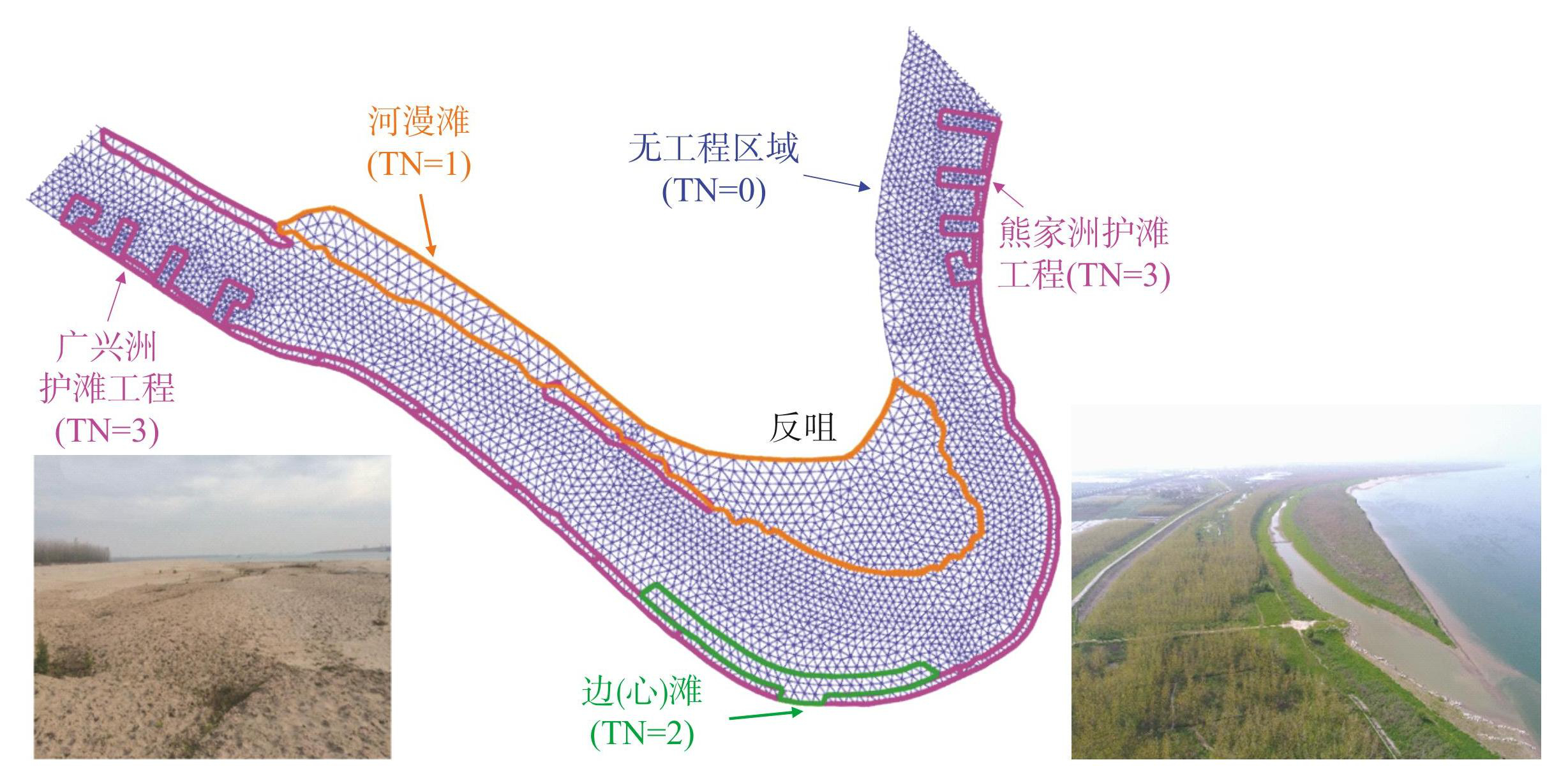
图1滩地、心滩或边滩及整治工程的区域划分

Fig.1Determining the zones of floodplain, channel bar, point bars and regulation works

1.2.2 输沙及河床冲淤计算的改进

在实施整治工程的区域，河床不发生冲刷，只能发生淤积，故针对标记为TN=3的单元输沙及冲淤计算与其他单元不同。当这些单元发生淤积时正常计算即可，当实施工程的单元发生冲刷时，以下几种情况冲淤厚度取值需要调整：（1）该单元发生冲刷，且单元上无淤积层提供泥沙时，应将该单元的冲淤厚度（ΔZ）取值为0；（2）该单元发生冲刷，且冲刷厚度大于单元整治工程上方淤积的可供冲刷厚度时，即ΔZ＞Z_b-Z₀（Z_b为此时单元河床高程，Z₀为单元初始高程）时，应将该单元的冲淤厚度取为Z_b-Z₀。在确定各单元的冲淤厚度后，根据冲淤厚度修改床沙级配和床沙特征参数，进而修正水流要素并根据悬移质输移方程和河床变形方程反算单元含沙量和水流挟沙力，最后将单元变量插值到各节点，用于下一时刻的计算。

1.3 考虑二次流影响的模块

在一般顺直段或分汊段的二维模拟中，扩散应力项的大小在量级上显著低于对流项、底坡项等，可忽略不计。然而在急弯段的二维模拟中，二次流的存在使得扩散应力项与其他项有大致相当的数量级，一般不可忽略^[15，20]。保留扩散应力项可反映二次流引起的动量交换。考虑扩散应力的影响时，模型新引入了u（z）和v（z）两个参数，需要补充u（z）、v（z）与u、v的计算关系才能使方程组封闭。已有研究提出了较多u（z）、v（z）与u、v的计算关系^[21-24]，其中de Vriend^[22]提出的流速垂向分布经验公式应用最为广泛，该公式中纵向流速的垂向分布采用的是对数流速分布，而横向流速的垂向分布则结合了对数流速分布和二次流的非线性分布，但没有考虑二次流与主流之间的非线性效应。已有研究表明，长江中游急弯段中二次流和主流之间的非线性作用不强^[25]，故本文采用de Vriend^[22]提出的模型计算扩散应力项，其中u（z）、v（z）的计算公式为：

u (z) = u [1 + \frac{\sqrt{g}}{κ C} + \frac{\sqrt{g}}{κ C} l n z] = u f_{m} (z)

(14)

v (z) = v f_{m} (z) + \frac{u h}{κ^{2} R} [2 F_{1} (z) + \frac{\sqrt{g}}{κ C} F_{2} (z) - 2 (1 - \frac{\sqrt{g}}{κ C}) f_{m} (z)]

(15)

式中，g为重力加速度；κ为卡门常数，κ=0.4；C为谢才系数；R为弯道曲率半径；f_m（z）、F₁（z）和F₂（z）的定义和计算方法见文献^[22]。将式（14）和式（15）代入式（12）和式（13）可得到扩散应力项的计算公式。式（15）中需要确定弯道曲率半径R，已有研究通常采用正交曲线网格模拟弯道水沙输移，其纵向的网格边界与河道中心线平行，而横向的网格线与河道中心线基本垂直，故每组垂直于水流方向的网格取河道中心线处的曲率半径即可。在无结构网格中，曲率半径的计算较为复杂，已有研究多采用试圆法计算得到的曲率半径作为整个弯道的曲率半径，不考虑曲率的沿程变化，难以精确考虑二次流的影响。

本文提出了一种适用于无结构网格的曲率半径确定方法（图2），具体计算步骤为：（ⅰ）计算研究河段河道中心线处的曲率。首先提取研究河段的岸边线，然后确定河道中心线，并将河道中心线上沿程散点之间的间距（Δs）设定为最小网格的边长，最后根据公式计算曲率的沿程变化，并进行平滑处理（图2a）；（ⅱ）网格生成后，按网格节点的编号从小到大确定所有网格节点的曲率。以节点A为例，首先检索与A点距离最小的河道中心线上的散点（B点，该点的曲率为1/R），A点的曲率近似取为1/R（图2b）；（ⅲ）基于网格节点处的曲率，确定所有网格单元的曲率。为方便处理，各网格单元处的曲率取3个网格节点处曲率的算数平均值。

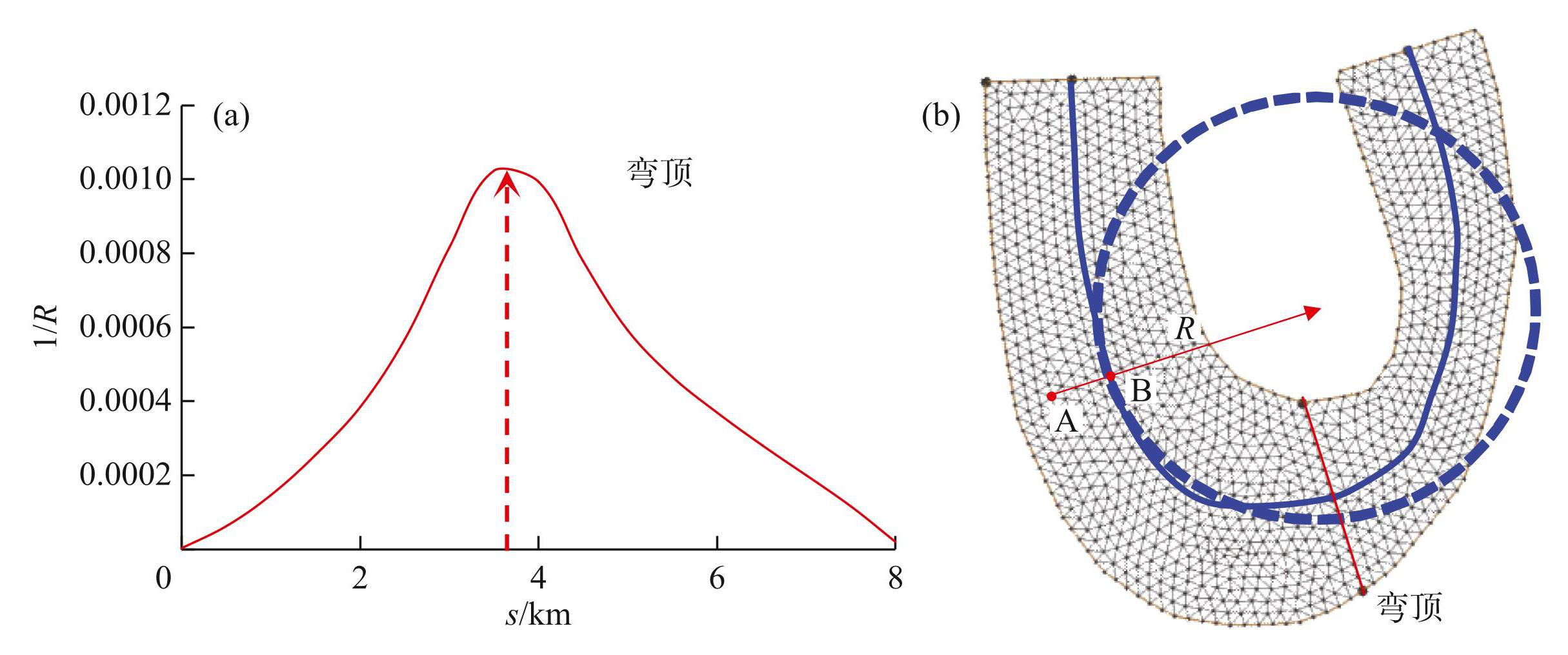
图2网格节点曲率取值方法：（a）河道中心线的曲率沿程变化；（b）节点的曲率

Fig.2Method for calculating the curvature at the mesh nodes: (a) longitudinal evolution of curvature along the channel centerline and （b） curvature at the mesh nodes

1.4 改进后模型的计算步骤

图3给出了考虑河道整治工程和二次流影响的二维水沙数学模型的计算步骤，主要包括:（ⅰ）生成网格，给网格节点赋予代码，同时确定单元的代码；（ⅱ）确定模型计算的初始和边界条件；（ⅲ）离散并求解水流连续方程和动量方程，并考虑二次流的影响，计算得到各单元的流速、水深等变量并插值到网格节点；（ⅳ）离散并求解非均匀悬沙不平衡输移方程，计算各单元的分组及总含沙量并插值到网格节点；（ⅴ）离散并求解河床变形方程，计算各单元分组沙冲淤厚度及总沙冲淤厚度并插值到网格节点，其中实施工程的区域需根据图中的原则调整冲淤厚度；（ⅵ）更新各单元和网格节点的河床高程，同时反算各单元和网格节点的含沙量和挟沙力，并调整单元床沙级配。（ⅶ）进行下一时刻的计算，直至计算结束。

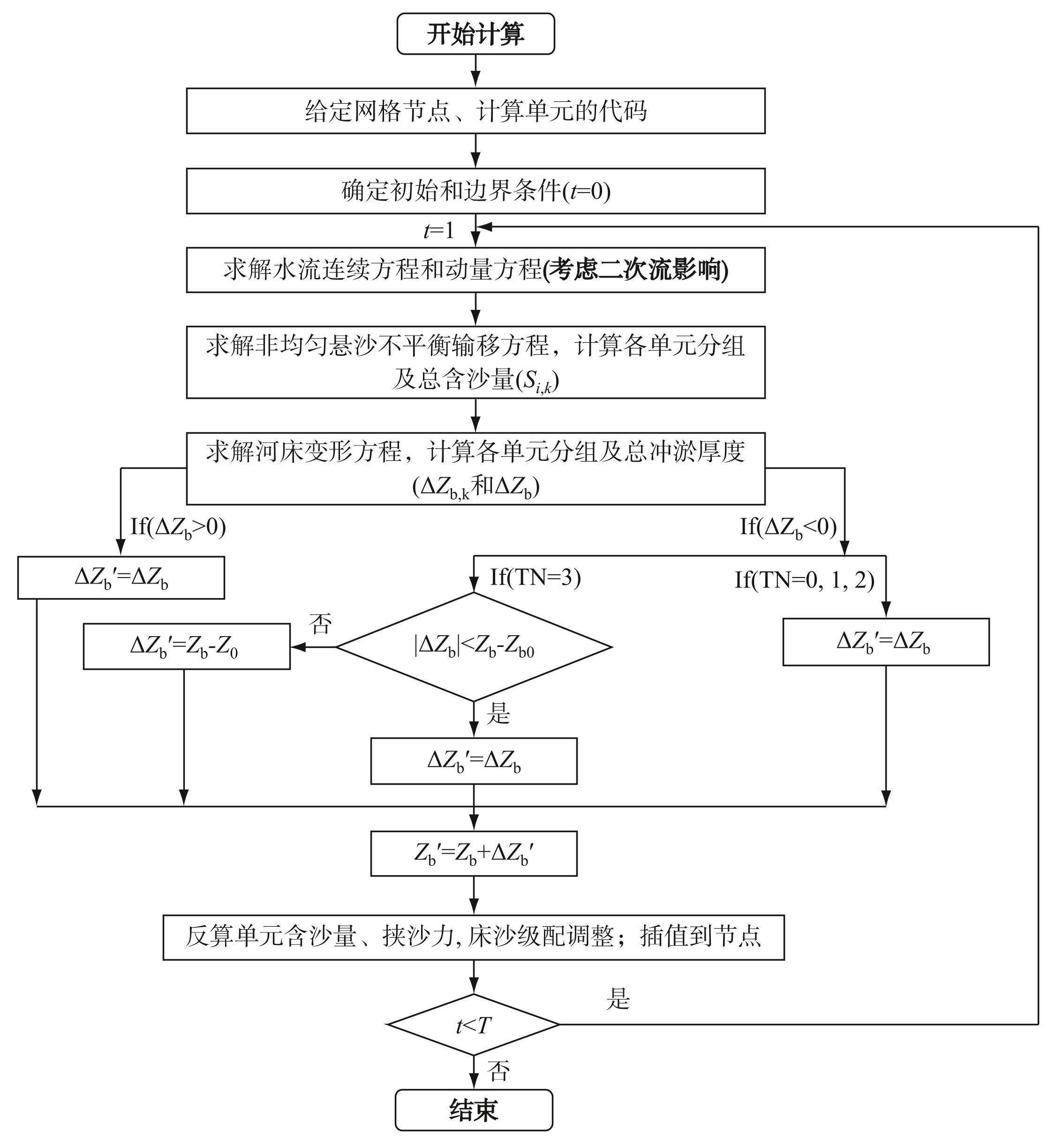
图3考虑河道整治工程和二次流影响的二维水沙数学模型的计算流程图

Fig.3Flow chart of the improved two-dimensional morphodynamic model considering the influence of regulation works and secondary flow

2 长江中游典型急弯段水沙输移及河床冲淤过程模拟

此处选取长江中游监利-城陵矶河段作为研究对象，采用该河段内水文站、水位站及典型急弯段的实测水沙以及整个河段的地形资料，计算急弯段的水沙输移及河床变形过程，对改进后的二维水沙数学模型进行率定与验证。

2.1 河段概况

下荆江监利-城陵矶河段全长约87 km，位于荆140至荆186之间，进口断面为监利水文站的观测断面，距上游三峡大坝约364 km，尾部与洞庭湖出流汇合，是荆江与洞庭湖交汇的江湖汇流河段（图4）。该河段为典型的弯曲河段，共由7个弯曲段及其过渡段组成，曲折系数约为1.9。监利河弯属于弯曲分汊段，反咀、七弓岭和观音洲弯道属于急弯段，其余弯道为微弯段。20世纪90年代以来，为控制河势、确保防洪和航运安全，水利及航道部门在该河段实施了大量的整治工程，包括沿江两岸的护岸工程，乌龟洲、广兴洲和熊家洲附近的护滩工程等（图4），故近年来河势总体保持稳定。局部河段河势仍在持续调整，上车湾、反咀、七弓岭和观音洲4个弯道发生凸冲凹淤现象，上车湾和反咀弯道形成了凹岸边滩，七弓岭和观音洲弯道形成了凹岸心滩。

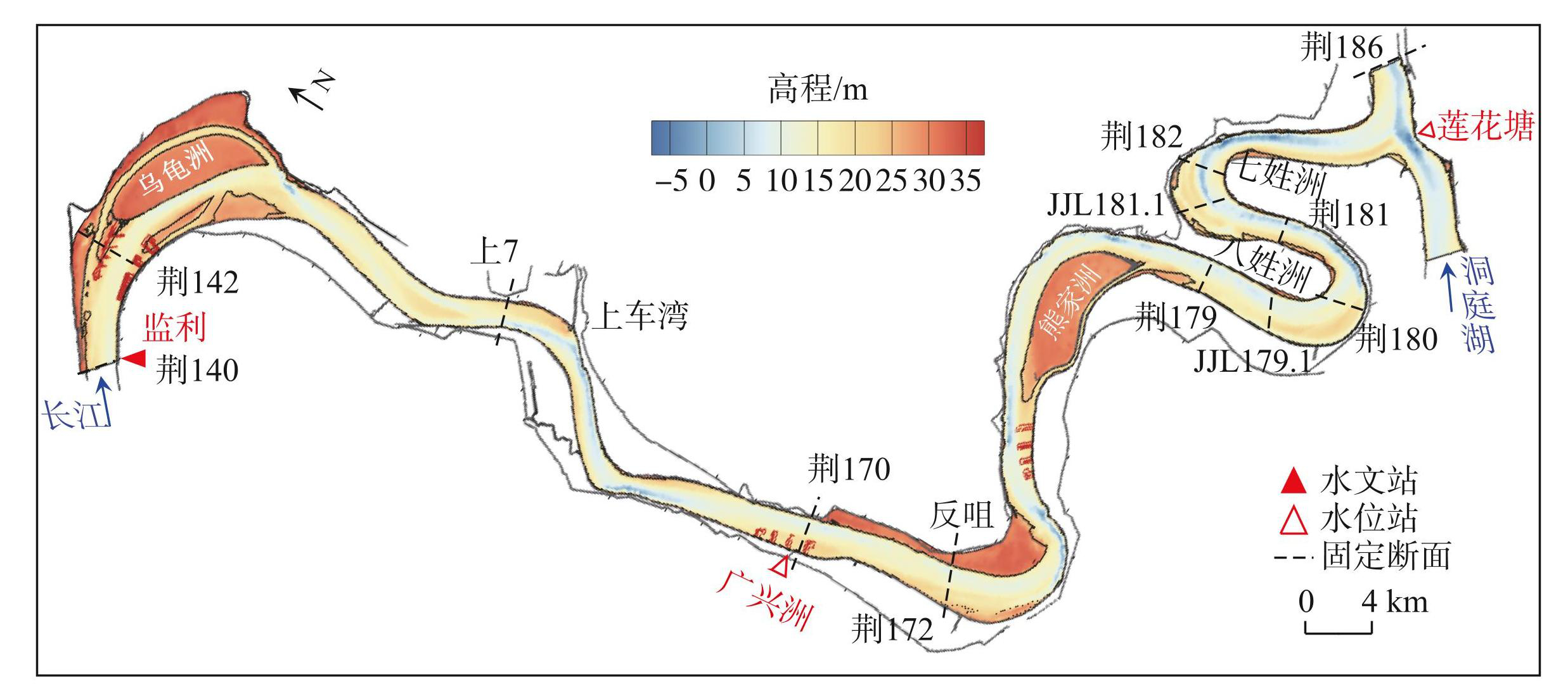
图4长江中游监利-城陵矶河段概况

Fig.4Sketch map of Jianli-Chenglingji reach of the middle Yangtze River

2.2 模型计算条件

2.2.1 进出口边界条件

监利站和七里山站分别为监利河段和洞庭湖出流的水沙控制站，故进口水沙过程分别采用上述两个水文站的实测数据。研究河段内设有广兴洲和莲花塘水位站，其日均水位资料可用于验证模型的计算结果。出口断面为荆186断面，位于荆江和洞庭湖汇流点的下游，其水位可采用莲花塘站和螺山站的日均水位插值得到。分别采用2014年和2018年研究河段内的实测水沙及地形数据对模型进行率定和验证，计算时间为5月1日-8月31日，计算条件如表1所示。另外收集了七弓岭-观音洲弯道中典型断面的水深、垂线平均流速及悬移质含沙量数据对模型的计算结果进行验证，上述数据源于长江委水文局。

表1模型率定及验证的计算条件

Tab.1 Calculation conditions of the model in calibration and verification

2.2.2 河床边界条件

河岸边界采用无滑移边界条件，即设定U和V均为0，且设定该处悬移质含沙量的横向梯度为0^[26]。首先将研究河段划分成三角形网格，并针对主槽区域和实施了整治工程的区域进行局部加密，共有20876个网格节点和39821个网格单元，网格单元的面积为1356~10050 m²，平均面积为3997 m²。河床设定为动床，初始地形分别采用2013年11月和2018年3月测量的长程河道地形。基于2014年10月和2017年10月监利-城陵矶河段的实测床沙级配数据，采用反距离插值法将固定断面床沙级配插值到网格节点上，作为模型率定和验证的初始床沙级配。需要说明的是，上述地形及床沙级配数据均源于长江委水文局。通常荆江河段测量了长程河道地形图的年份不再对固定断面的床沙进行取样，因此本文选取了临近年份的床沙级配实测数据作为模型的初始床沙级配。

2.2.3 动边界处理及模型参数设置

本文参考夏军强等^[27]的研究，采用冻结法处理动边界问题。考虑到长江中游来沙量较低，故模型中水流与泥沙的计算为非耦合模式。根据网格尺寸，为确保全局网格均满足CFL条件，将时间步长设定为0.5 s。主槽糙率系数取0.018~0.025，滩地糙率系数取0.03~0.04。水流挟沙力采用张瑞瑾挟沙力公式，式中参数k取0.02~0.035，m取1.05。恢复饱和系数取为经验参数，河床发生冲刷时取0.4，发生淤积时取0.2，冲淤相对平衡时取0.3，水温设为20℃，床沙干密度ρ′=1400 kg/m³。需要说明的是，张瑞瑾挟沙力公式中参数k和m以及恢复饱和系数的取值均参考Zhou等^[28]的研究赋初值，并根据典型断面的实测含沙量进行率定。另外主槽和滩地糙率系数的初值也根据Zhou等^[28]的研究给定，并基于计算区域内广兴洲水位站的实测数据进行率定。

2.3 典型断面的模拟结果

2.3.1 水位过程的率定与验证结果

图5给出了率定和验证工况中广兴洲站的水位模拟结果，率定和验证工况中，广兴洲站水位的绝对误差范围分别为-0.36~0.14 m、-0.55~0.77 m，纳什效率系数分别为0.987、0.974，表明模型对水位的模拟精度较高。

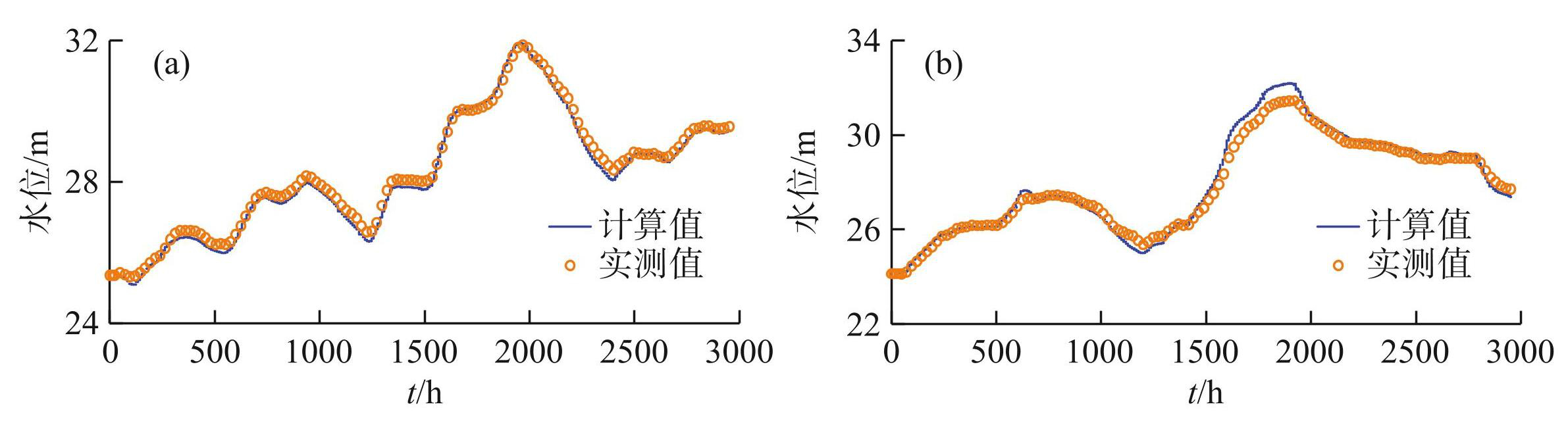
图5广兴洲站水位计算与实测过程对比:（a）率定工况;（b）验证工况

Fig.5Comparisons between the calculated and measured water level hydrographs at Guangxingzhou station in the calibration (a) and verification (b)

2.3.2 水深、垂线平均流速和含沙量的率定与验证结果

图6给出了率定工况中七弓岭-观音洲弯道3个典型断面（断面位置见图4）水深、垂线平均流速及含沙量的模拟结果，实测值的测量时间均为2014年8月16日，对应监利站的流量为20300 m³/s。各断面水深的横向分布拟合较好，荆180断面右岸存在凹岸心滩，水深从左到右先减小后增大，计算最小水深为8.7 m，位于距离左岸1018 m处，而实测最小水深为6.4 m，位置距离左岸约905 m，两者基本吻合。荆182断面最大水深的计算值在数值和位置上均与实测值符合较好，但左岸局部位置的计算误差相对较大，原因是近岸地形变化较大，而实测水下地形的精度有限，通常横向实测高程点的间隔约为50~80 m，精度远低于1∶5000的汛后固定断面地形，而近岸网格尺寸难以精确与高程点的间距匹配，导致地形插值产生误差。垂线平均流速的横向分布与实测值同样符合较好，荆179断面垂线平均流速的实测值均分布在计算值的周围，两者符合最好。荆180断面1700~2000 m处垂线平均流速的实测值显著高于计算值。此外，荆182断面实测流速表明左岸存在回流区，模拟的流速分布也存在回流区，但回流区内的流速略小于实测值。

图7给出了验证工况中七弓岭-观音洲弯道中典型断面水深、垂线平均流速及含沙量计算与实测值的对比结果。水深计算值与实测值的横向分布基本相符，但数值上仍存在一定的误差，如荆180断面右岸最大水深接近16 m，而实测值为10 m。产生误差的主要原因有两个方面，一是该断面右岸地形变化较大，插值后深泓高程相差约4 m，导致了水深的误差；二是七弓岭江段河岸上的实测点较少，且部分区域未测量堤顶高程，故地形插值后可能导致部分河岸的堤顶高程偏低，也会导致计算水深偏小。各断面垂线平均流速的计算值与实测值总体符合较好，但荆179断面右岸附近计算流速偏小，而荆180断面主槽区域的计算流速偏大。荆182断面的左岸附近存在回流区，尽管模拟的流速分布中也存在反向流速，但其值略小于实测值，且荆182断面主槽区域的模拟流速比实测流速更大，存在一定的计算误差。垂线平均含沙量的计算误差高于水深和流速，如荆180断面右岸附近含沙量计算值明显低于实测值；荆182断面主槽区域垂线平均含沙量的模拟结果较好，但回流区内计算值略低于实测值。

图6和图7同时对比了模型改进前、后的计算结果，总体而言模型改进后计算精度有所提高。在弯道过渡段，如图6和图7中的荆179断面，考虑和不考虑扩散应力项的垂线平均流速和含沙量分布相差不大。在弯曲段，增加考虑扩散应力项后垂线平均流速和含沙量横向分布的计算精度更高。图6中荆182断面分离区内的流速分布更接近实测值。图7中荆180断面右岸凹岸心滩附近的流速和左岸主槽区域垂线平均含沙量的计算精度均显著提升，荆182断面流速分布的模拟结果也有一定程度的改善。

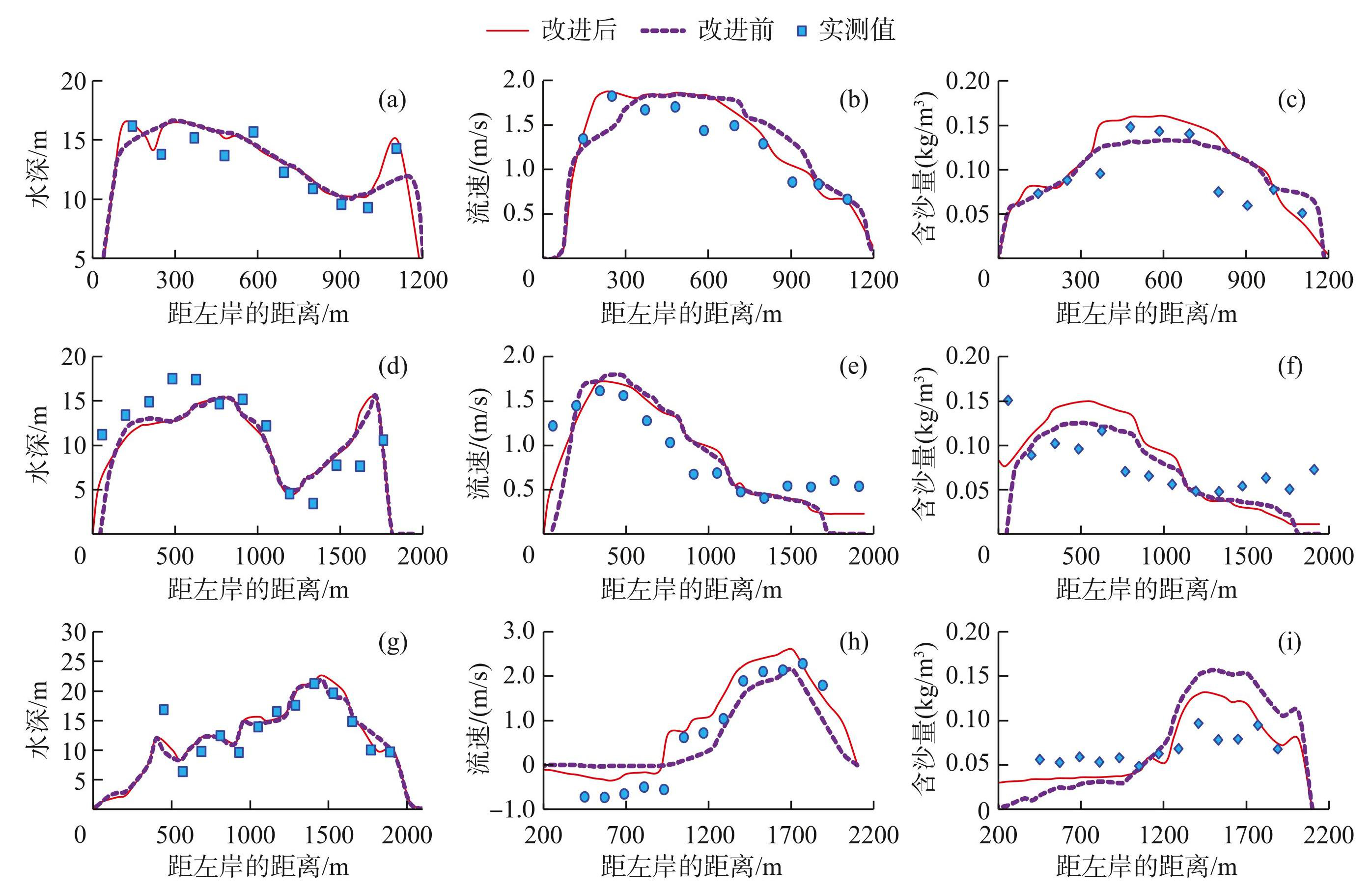
图6率定工况典型断面计算与实测的水深、垂线平均流速及含沙量对比:（a~c）荆179;（d~f）荆180;（g~i）荆182

Fig.6Comparisons of the calculated and measured water depths, depth-averaged velocities, and suspended sediment concentrations at typical cross sections of Jing179 (a-c) , Jing180 (d-f) , and Jing182 (g-f) in calibration

2.4 急弯段特定流量下的流速和含沙量分布

2.4.1 垂线平均流速的横向分布

图8给出了率定和验证工况中20000 m³/s流量下研究河段内的主流线沿程摆动情况及典型急弯段（七弓岭和观音洲弯道）的流速分布。尽管率定与验证工况中地形为不同年份，但滩槽格局没有显著变化，故同流量下流速分布也非常相似。总体而言，各弯曲段主流线均由凸岸向凹岸摆动，符合一般规律，同时主流线横向摆动滞后于地形的调整。急弯段弯顶上游的主流线偏靠凸岸，在弯顶下游才向凹岸摆动，而一般急弯段中主流线通常在弯顶上游向凹岸摆动。此外，观音洲弯道凹岸弯顶上游和凸岸弯顶下游均存在回流区。

考虑到两组工况的流速分布相似，此处选取验证工况中的典型断面（七弓岭弯道的荆180和观音洲断面荆182）分析垂线平均流速的横向分布特点。图9给出了不同流量下2个典型断面垂线平均流速的横向分布以及当年5—8月的断面形态变化。荆180和荆182断面凹岸附近均存在心滩，主槽偏靠凸岸，断面形态为“W”型。荆180断面高流速区位于凹岸心滩左侧，而荆182断面的高流速区位于凹岸心滩的右侧，表明高流速区偏靠凸岸，凹岸附近的流速较小，故横向流速梯度较大。随着流量的增大，高流速区向凸岸摆动。此外，高流速区与冲刷区重合，而淤积区与分离区重合，表明本模型可用于模拟急弯段的流速分布。

2.4.2 垂线平均含沙量的横向分布

从图10a可以看出，验证工况中七弓岭-观音洲弯道20000 m³/s流量下的2个弯道含沙量分布不对称，上游过渡段、弯顶上段和弯顶下段的含沙量均呈现凸岸高于凹岸的特点。究其原因，七弓岭和观音洲弯道主要过流通道均偏靠凸岸，而凹岸都形成了发育程度较高的心滩，有效输沙宽度明显减小。此处引入无量纲参数G_s表征垂线平均含沙量的横向梯度：

G_{s} = \partial (S_{i} / S_{c s}) / \partial n

(16)

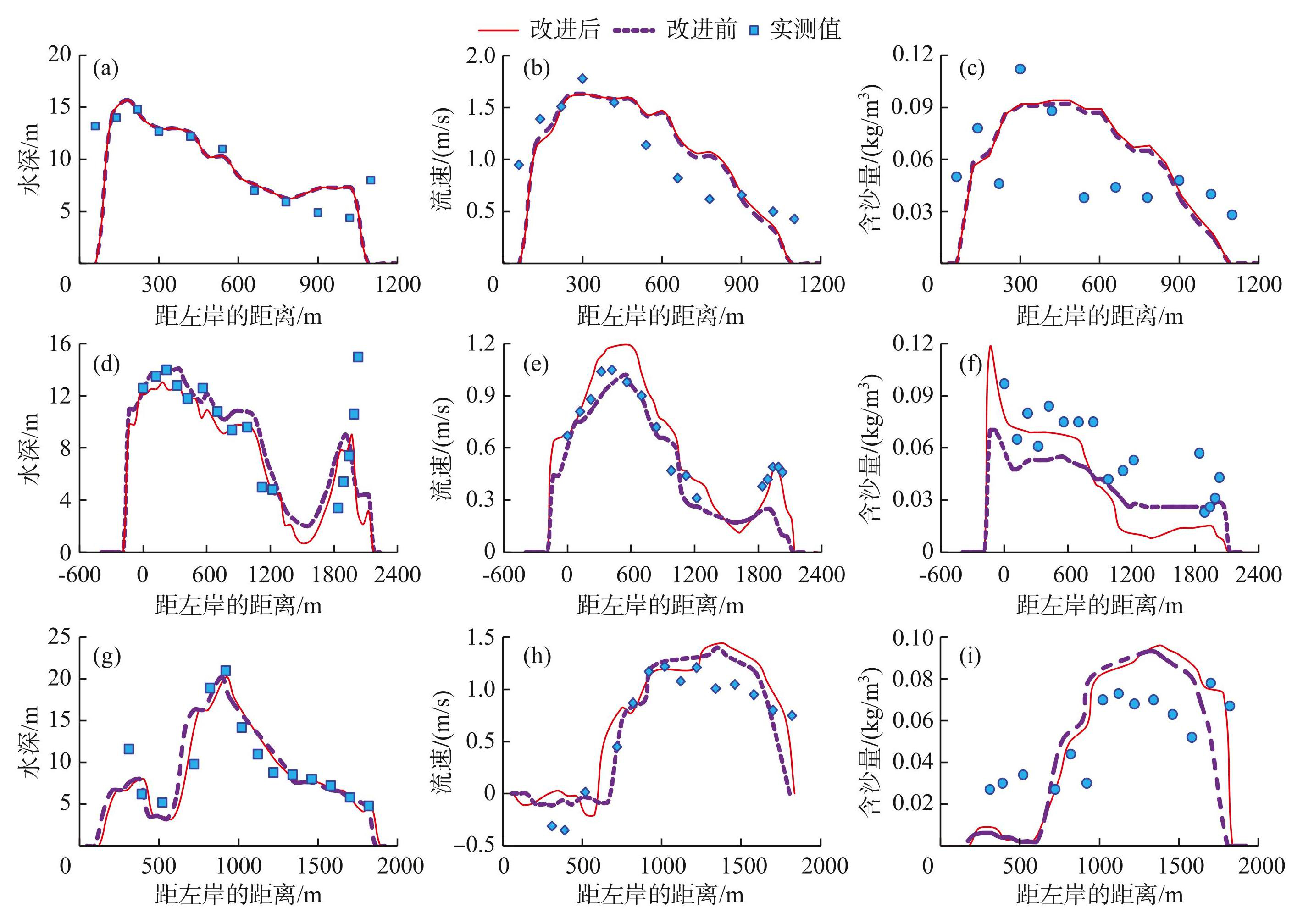
图7验证工况典型断面计算与实测的水深、垂线平均流速及含沙量对比:（a~c）荆179;（d~f）荆180;（g~i）荆182

Fig.7Comparisons of the calculated and measured water depths, depth-averaged velocities, and suspended sediment concentrations at typical cross sections of Jing179 (a-c) , Jing180 (d-f) , and Jing182 (g-i) in verification

式中，S_i为断面上各网格单元的垂线平均含沙量，kg/m³；S_cs为断面平均含沙量，kg/m³；n为各网格点与左岸的距离，km。从图10b、c可以看出，荆180和荆182断面的最大含沙量均偏靠凸岸，且与冲刷区重合。荆180断面G_s随着流量的增大而增大，表明流量越大，含沙量横向梯度越大。荆182断面G_s则随着流量的增大而减小，表明流量越大，含沙量横向梯度越小。

2.4.3 急弯段河床冲淤分布

图11给出了率定和验证工况下整个河段的冲淤分布，除弯曲段外其他区域的冲淤幅度不大，以七弓岭-观音洲弯道的冲淤幅度最大。率定工况中，七弓岭弯道呈现凸冲凹淤的特点，而观音洲弯道中弯顶上段以淤积为主，下段凸冲凹淤。验证工况中，七弓岭弯道以淤积为主，仅在弯顶区域凸岸近岸河床略有冲刷，其他区域均为淤积。观音洲弯道的调整仍在继续，凸岸边滩仍保持冲刷状态，淤积区位于河道中部，凹岸心滩的冲淤幅度较小。尽管总体上七弓岭和观音洲弯道呈现凸冲凹淤演变模式，但不同水沙条件下冲淤分布呈现不同的特点。

3 结论

为更准确地模拟急弯段的水沙输移及河床冲淤过程，包括流速分布、含沙量分布及河床变形等，本文针对基于无结构网格有限体积法的平面二维水沙动力学模型进行了改进，并将改进后的模型应用到长江中游监利-城陵矶河段。主要结论如下：

1）在基于无结构网格有限体积法的平面二维水沙数学模型中，新增了考虑整治工程和二次流影响的计算模块，构建了适用于急弯段的二维水沙动力学模型，并采用OpenMP并行技术提高模型的计算效率。首先对模型整个计算区域中实施了整治工程的区域进行代码标记，在计算过程中实施了整治工程且前期模拟未形成可冲层的区域不发生冲刷，从而考虑整治工程的影响；同时模型中计算了扩散应力项，用于考虑二次流对急弯段垂线平均流速横向分布的影响。

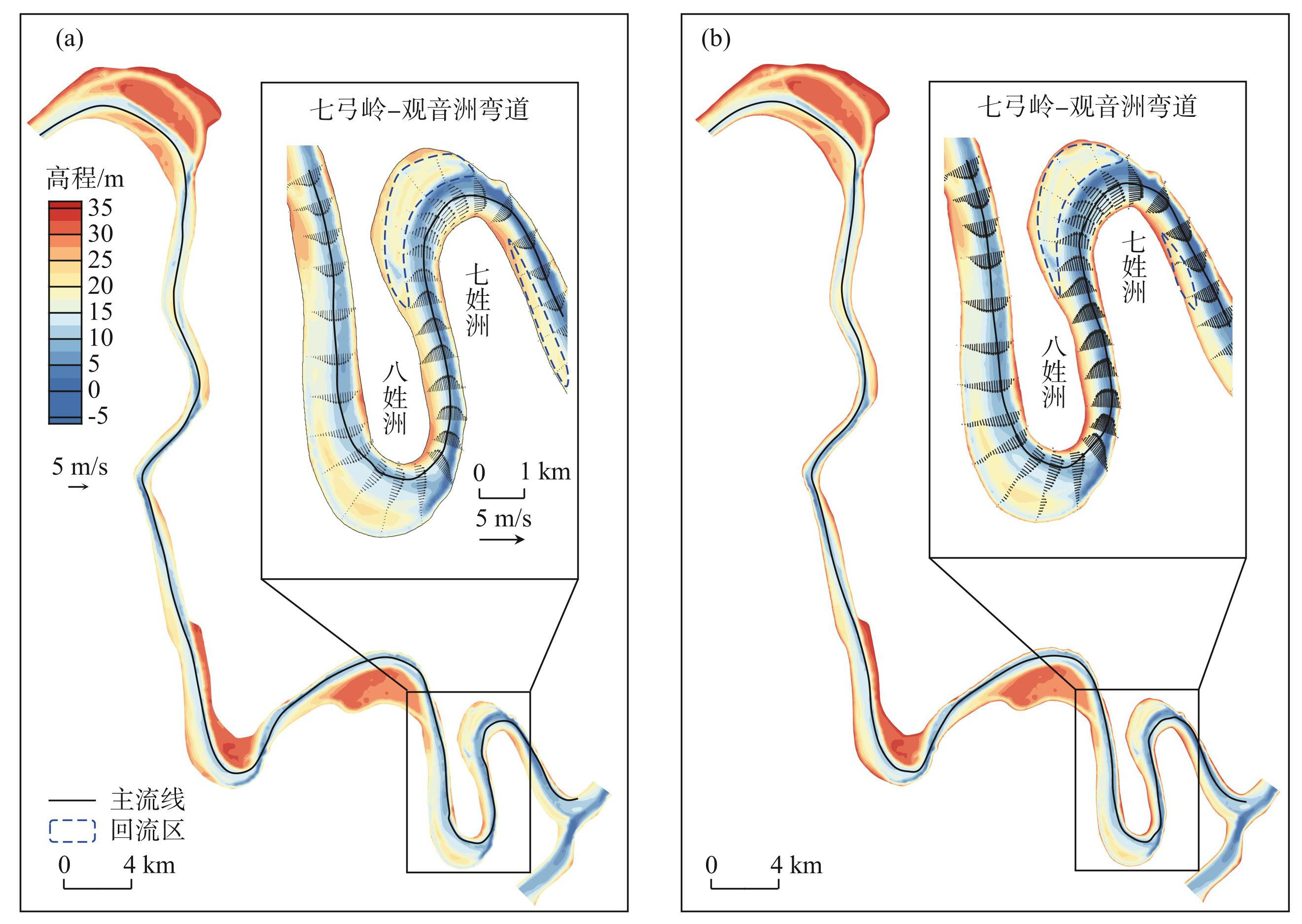
图8监利-城陵矶河段20000 m³/s流量下主流线变化:（a）率定工况;（b）验证工况

Fig.8Shift of the mainstream at the discharge of 20000 m³/s in the Jianli-Chenglingji reach in calibration (a) and verification (b)

图9验证工况中急弯段典型断面不同流量下垂线平均流速的横向分布:（a）荆180;（b）荆182

Fig.9Lateral distribution of the depth-averaged velocity at typical cross sections of Jing180 (a) and Jing182 (b) under different discharges around the sharp bends in verification

2）基于2014年和2018年下荆江监利-城陵矶河段的实测水沙资料对模型进行率定和验证，计算结果表明：广兴洲站水位过程的纳什效率系数在0.97以上，急弯段典型断面水深、垂线平均流速及含沙量横向分布的计算值与实测值符合较好，故改进后的模型可以较准确地模拟急弯段水沙输移过程。

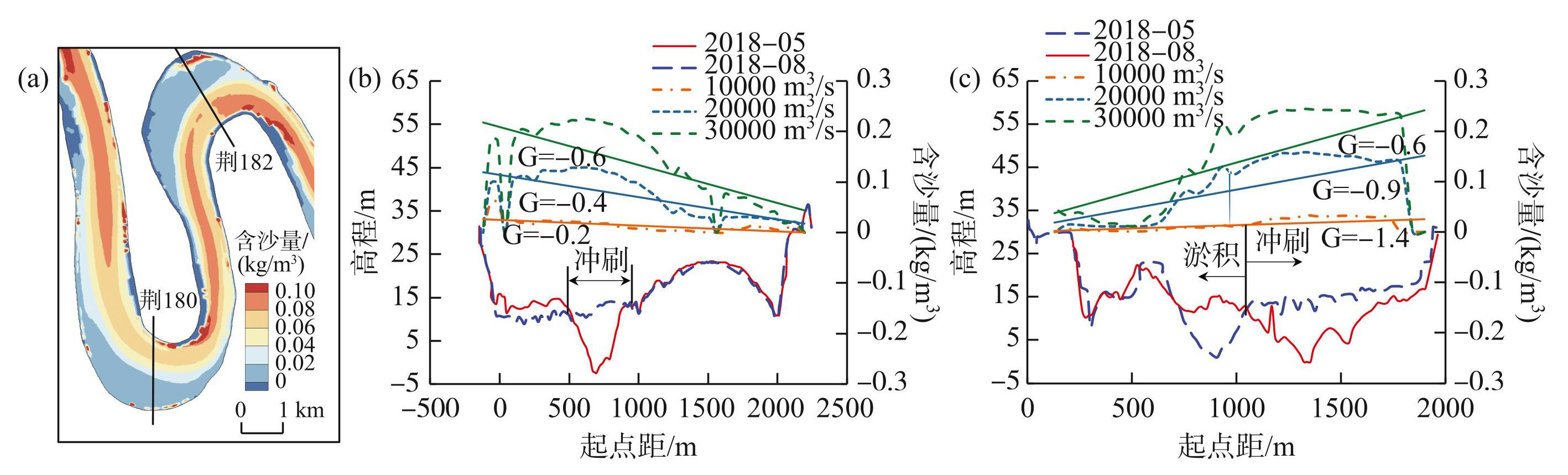
图10验证工况中七弓岭-观音洲弯道不同流量下的含沙量分布:（a）七弓岭-观音洲弯道;（b）荆180;（c）荆182

Fig.10Lateral distribution of the depth averaged suspended sediment concentration at different discharges around the Qigongling-Guanyinzhou bends (a) , and at typical cross sections of Jing180 (b) and Jing182 (c) in verification

图11率定和验证工况下研究河段的冲淤分布:（a）率定工况;（b）验证工况

Fig.11Distribution of deformation depth in the study reach in calibration (a) and verification (b)

3）急弯段弯顶上段的主流线偏靠凸岸，在弯顶下段才向凹岸摆动，主流摆动过程比一般急弯段的滞后程度更高。此外，观音洲弯道凹岸弯顶上段和凸岸弯顶下段均存在回流区。七弓岭和观音洲弯道含沙量均呈现凸岸高于凹岸的特点，且河床总体呈现凸冲凹淤的特点。

尽管模型采用了OpenMP并行技术提高了计算效率，但受限于CFL条件，只能采用全局最小时间步长，后期将采用局部时间步长等技术提高模型的计算效率。

图1滩地、心滩或边滩及整治工程的区域划分

Fig.1Determining the zones of floodplain, channel bar, point bars and regulation works

下载: 全尺寸图片

图2网格节点曲率取值方法：（a）河道中心线的曲率沿程变化；（b）节点的曲率

Fig.2Method for calculating the curvature at the mesh nodes: (a) longitudinal evolution of curvature along the channel centerline and （b） curvature at the mesh nodes

下载: 全尺寸图片

图3考虑河道整治工程和二次流影响的二维水沙数学模型的计算流程图

Fig.3Flow chart of the improved two-dimensional morphodynamic model considering the influence of regulation works and secondary flow

下载: 全尺寸图片

图4长江中游监利-城陵矶河段概况

Fig.4Sketch map of Jianli-Chenglingji reach of the middle Yangtze River

下载: 全尺寸图片

图5广兴洲站水位计算与实测过程对比:（a）率定工况;（b）验证工况

Fig.5Comparisons between the calculated and measured water level hydrographs at Guangxingzhou station in the calibration (a) and verification (b)

下载: 全尺寸图片

图6率定工况典型断面计算与实测的水深、垂线平均流速及含沙量对比:（a~c）荆179;（d~f）荆180;（g~i）荆182

下载: 全尺寸图片

图7验证工况典型断面计算与实测的水深、垂线平均流速及含沙量对比:（a~c）荆179;（d~f）荆180;（g~i）荆182

下载: 全尺寸图片

图8监利-城陵矶河段20000 m³/s流量下主流线变化:（a）率定工况;（b）验证工况

Fig.8Shift of the mainstream at the discharge of 20000 m³/s in the Jianli-Chenglingji reach in calibration (a) and verification (b)

下载: 全尺寸图片

图9验证工况中急弯段典型断面不同流量下垂线平均流速的横向分布:（a）荆180;（b）荆182

Fig.9Lateral distribution of the depth-averaged velocity at typical cross sections of Jing180 (a) and Jing182 (b) under different discharges around the sharp bends in verification

下载: 全尺寸图片

图10验证工况中七弓岭-观音洲弯道不同流量下的含沙量分布:（a）七弓岭-观音洲弯道;（b）荆180;（c）荆182

下载: 全尺寸图片

图11率定和验证工况下研究河段的冲淤分布:（a）率定工况;（b）验证工况

Fig.11Distribution of deformation depth in the study reach in calibration (a) and verification (b)

下载: 全尺寸图片

表1模型率定及验证的计算条件

下载: 全尺寸图片

图1滩地、心滩或边滩及整治工程的区域划分

Fig.1Determining the zones of floodplain, channel bar, point bars and regulation works

图2网格节点曲率取值方法：（a）河道中心线的曲率沿程变化；（b）节点的曲率

Fig.2Method for calculating the curvature at the mesh nodes: (a) longitudinal evolution of curvature along the channel centerline and （b） curvature at the mesh nodes

图3考虑河道整治工程和二次流影响的二维水沙数学模型的计算流程图

Fig.3Flow chart of the improved two-dimensional morphodynamic model considering the influence of regulation works and secondary flow

图4长江中游监利-城陵矶河段概况

Fig.4Sketch map of Jianli-Chenglingji reach of the middle Yangtze River

图5广兴洲站水位计算与实测过程对比:（a）率定工况;（b）验证工况

Fig.5Comparisons between the calculated and measured water level hydrographs at Guangxingzhou station in the calibration (a) and verification (b)

图6率定工况典型断面计算与实测的水深、垂线平均流速及含沙量对比:（a~c）荆179;（d~f）荆180;（g~i）荆182

图7验证工况典型断面计算与实测的水深、垂线平均流速及含沙量对比:（a~c）荆179;（d~f）荆180;（g~i）荆182

图8监利-城陵矶河段20000 m³/s流量下主流线变化:（a）率定工况;（b）验证工况

Fig.8Shift of the mainstream at the discharge of 20000 m³/s in the Jianli-Chenglingji reach in calibration (a) and verification (b)

图9验证工况中急弯段典型断面不同流量下垂线平均流速的横向分布:（a）荆180;（b）荆182

Fig.9Lateral distribution of the depth-averaged velocity at typical cross sections of Jing180 (a) and Jing182 (b) under different discharges around the sharp bends in verification

图10验证工况中七弓岭-观音洲弯道不同流量下的含沙量分布:（a）七弓岭-观音洲弯道;（b）荆180;（c）荆182

图11率定和验证工况下研究河段的冲淤分布:（a）率定工况;（b）验证工况

Fig.11Distribution of deformation depth in the study reach in calibration (a) and verification (b)

表1模型率定及验证的计算条件

图1滩地、心滩或边滩及整治工程的区域划分

Fig.1Determining the zones of floodplain, channel bar, point bars and regulation works

图2网格节点曲率取值方法：（a）河道中心线的曲率沿程变化；（b）节点的曲率

Fig.2Method for calculating the curvature at the mesh nodes: (a) longitudinal evolution of curvature along the channel centerline and （b） curvature at the mesh nodes

图3考虑河道整治工程和二次流影响的二维水沙数学模型的计算流程图

Fig.3Flow chart of the improved two-dimensional morphodynamic model considering the influence of regulation works and secondary flow

图4长江中游监利-城陵矶河段概况

Fig.4Sketch map of Jianli-Chenglingji reach of the middle Yangtze River

图5广兴洲站水位计算与实测过程对比:（a）率定工况;（b）验证工况

Fig.5Comparisons between the calculated and measured water level hydrographs at Guangxingzhou station in the calibration (a) and verification (b)

图6率定工况典型断面计算与实测的水深、垂线平均流速及含沙量对比:（a~c）荆179;（d~f）荆180;（g~i）荆182

图7验证工况典型断面计算与实测的水深、垂线平均流速及含沙量对比:（a~c）荆179;（d~f）荆180;（g~i）荆182

图8监利-城陵矶河段20000 m³/s流量下主流线变化:（a）率定工况;（b）验证工况

Fig.8Shift of the mainstream at the discharge of 20000 m³/s in the Jianli-Chenglingji reach in calibration (a) and verification (b)

图9验证工况中急弯段典型断面不同流量下垂线平均流速的横向分布:（a）荆180;（b）荆182

Fig.9Lateral distribution of the depth-averaged velocity at typical cross sections of Jing180 (a) and Jing182 (b) under different discharges around the sharp bends in verification

图10验证工况中七弓岭-观音洲弯道不同流量下的含沙量分布:（a）七弓岭-观音洲弯道;（b）荆180;（c）荆182

图11率定和验证工况下研究河段的冲淤分布:（a）率定工况;（b）验证工况

Fig.11Distribution of deformation depth in the study reach in calibration (a) and verification (b)

表1模型率定及验证的计算条件

Nanson RA. Flow fields in tightly curving meander bends of low width-depth ratio. Earth Surface Processes and Landforms,2010,35(2):119-135. DOI:10.1002/esp.1878.

Schwendel AC, Nicholas AP, Aalto RE et al. Interaction between meander dynamics and floodplain heterogeneity in a large tropical sand-bed river: The Rio Beni, Bolivian Amazon. Earth Surface Processes and Landforms,2015,40(15):2026-2040. DOI:10.1002/esp.3777.

Blanckaert K,de Vriend HJ. Meander dynamics: A nonlinear model without curvature restrictions for flow in open-channel bends. Journal of Geophysical Research: Earth Surface,2010,115(F4): F04011. DOI:10.1029/2009JF001301.

Xu D, Bai YC, Tan Y. Research progress of meandering river dynamic development. Journal of Sediment Research,2011,(4):73-80.[许栋, 白玉川, 谭艳. 蜿蜒河流演变动力过程及其研究进展. 泥沙研究,2011,(4):73-80.]

Xia JQ, Wang GQ. Numerical simulation of flow and bed deformation in meandering rivers considering the erosion of bank. Journal of Hydraulic Engineering,2002,33(6):60-66.[夏军强, 王光谦. 考虑河岸冲刷的弯曲河道水流及河床变形的数值模拟. 水利学报,2002,33(6):60-66.]

Deng SS, Xia JQ, Zhou MR. Coupled two-dimensional modeling of bed evolution and bank erosion in the upper Jingjiang reach of middle Yangtze River. Geomorphology,2019,344:10-24. DOI:10.1016/j.geomorph.2019.07.010.

Crosato A. Analysis and modelling of river meandering. Amsterdam: Ios Press,2008.

Duan JG, Julien PY. Numerical simulation of meandering evolution. Journal of Hydrology,2010,391(1/2):34-46. DOI:10.1016/j.jhydrol.2010.07.005.

Turnipseed C, Konsoer K, Richards D et al. Numerical modeling of two-dimensional hydrodynamics in a highly curving and actively evolving neck cutoff under different hydrologic conditions. Water Resources Research,2021,57(2):e2020WR027329. DOI:10.1029/2020WR027329.

Hu P, Lei YL, Han JJ et al. Computationally efficient modeling of hydro-sediment-morphodynamic processes using a hybrid local time step/global maximum time step. Advances in Water Resources,2019,127:26-38. DOI:10.1016/j.advwatres.2019.03.006.

Hu P, Lei YL, Deng SY et al. Role of bar-channel interactions in a dominant branch shift: The Taipingkou waterway, Yangtze River, China. River Research and Applications,2021,37(3):494-508. DOI:10.1002/rra.3761.

Lyu BH, Li J, Hu P et al. High-resolution hydro-sediment-morphodynamic modelling of a meandering river reach with mid-channel bars on multiyear timescales: A case study of Shashi Reach in Middle Yangtze River. Journal of Hydrology,2024,635:131167. DOI:10.1016/j.jhydrol.2024.131167.

Olsen NRB. Three-dimensional CFD modeling of self-forming meandering channel. Journal of Hydraulic Engineering,2003,129(5):366-372. DOI:10.1061/(asce)0733-9429(2003)129:5(366).

Jia DD, Shao XJ, Wang H et al.3D numerical simulation of fluvial processes in the Shishou bend during the early filling of the Three Gorges Reservoir. Advances in Water Science,2010,21(1):43-49.[假冬冬, 邵学军, 王虹等. 三峡工程运用初期石首河弯河势演变三维数值模拟. 水科学进展,2010,21(1):43-49.]

Begnudelli L, Valiani A, Sanders BF. A balanced treatment of secondary currents,turbulence and dispersion in a depth-integrated hydrodynamic and bed deformation model for channel bends. Advances in Water Resources,2010,33(1):17-33. DOI:10.1016/j.advwatres.2009.10.004.

Fraccarollo L, Toro EF. Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems. Journal of Hydraulic Research,1995,33(6):843-864. DOI:10.1080/00221689509498555.

Duran A, Liang Q, Marche F. On the well-balanced numerical discretization of shallow water equations on unstructured meshes. Journal of Computational Physics,2013,235:565-586. DOI:10.1016/j.jcp.2012.10.033.

Valiani A, Begnudelli L. Divergence form for bed slope source term in shallow water equations. Journal of Hydraulic Engineering,2006,132(7):652-665. DOI:10.1061/(asce)0733-9429(2006)132:7(652).

谭维炎. 计算浅水动力学有限体积法的应用. 北京: 清华大学出版社,1998.

Zhou G, Yao SM, Qin CC et al. Comparative evaluation of secondary flow correction methods for consecutive bend flow simulation. Advances in Water Science,2016,27(2):266-279.[周刚, 姚仕明, 秦翠翠等. 连续弯道水流模拟中二次流修正效果评价. 水科学进展,2016,27(2):266-279.]

Rozovskii IL. Flow of water in bends of open channels. Kiev: Academy of Sciences of the Ukrainian SSR,1957.

de Vriend HJ. A mathematical model of steady flow in curved shallow channels. Journal of Hydraulic Research,1977,15(1):37-54. DOI:10.1080/00221687709499748.

Bernard R. STREMR: Numerical model for depth-averaged incompressible flow. US Army Corps of Engineers,1993

Lien HC, Hsieh TY, Yang JC et al. Bend-flow simulation using 2D depth-averaged model. Journal of Hydraulic Engineering,1999,125(10):1097-1108. DOI:10.1061/(asce)0733-9429(1999)125:10(1097).

Deng SS, Xia JQ, Zhou MR et al. Secondary flow and flow redistribution in two sharp bends on the middle Yangtze River. Water Resources Research,2021,57(10):e2020WR028534. DOI:10.1029/2020WR028534.

Xia JQ, Lin BL, Falconer RA et al. Modelling dam-break flows over mobile beds using a 2D coupled approach. Advances in Water Resources,2010,33(2):171-183. DOI:10.1016/j.advwatres.2009.11.004.

夏军强, 王光谦, 吴保生. 平面二维河床纵向与横向变形数学模型. 中国科学E辑: 技术科学,2004,(S1):165-174.

Zhou MR, Xia JQ, Deng SS et al. Two-dimensional modeling of channel evolution under the influence of large-scale river regulation works. International Journal of Sediment Research,2022,37(4):424-434. DOI:10.1016/j.ijsrc.2022.02.005.