摘要
流域水文模型参数对水文模拟预报的精度具有重要影响。在水文模型的数学表达由差分形式向微分形式发展的背景下,如何利用微分形式水文模型过程连续、时间尺度灵活的特点进行模型参数优化是值得研究的问题。本文提出一种基于神经常微分方程(NODE)的水文模型参数优化方法,将神经网络嵌入水文模型的微分动力系统,使用常微分方程数值求解器正向模拟连续水文过程,计算损失函数并反向传播梯度信息以更新神经网络参数,从而实现水文模型参数优化。以新安江模型为例,设计了理想数值实验和典型流域应用两种验证方案,并与SCE-UA优化方法进行了对比。结果显示,基于NODE优化方法确定的新安江模型参数,与理想参数“真值”的误差平均不超过9.8%;相较于SCE-UA方法,NODE得到的优化参数对流量过程具有更高的模拟精度。研究表明,基于NODE的参数优化方法通过微分方程正向求解和梯度信息反向传播,可有效搜索参数空间,适用于微分形式水文模型的参数优化问题。
Abstract
The parameters of watershed hydrological models significantly influence the accuracy of hydrological simulation and forecast. In the context of hydrological model expressions evolving from discrete to differential forms, it is worth investigating how to utilize the continuous process and flexible time scales of differential hydrological models for parameter optimization. A hydrological model parameter optimization method based on neural ordinary differential equations (NODE) is proposed, in which the neural network is embedded into the differential dynamical system of the hydrological model, and the continuous hydrological process is simulated forward using the ordinary differential equation numerical solver. The loss function is calculated, and the gradient information is propagated backward to update the neural network parameters, thereby optimizing the hydrological model parameters. Taking parameter optimization of the Xin'anjiang model as an example, an ideal numerical experiment and typical watershed application are conducted for validation and compared with the SCE-UA optimization method. The results show that the average error between the Xin'anjiang model parameters determined by the NODE optimization method and the ideal parameter ‘true value’ is not more than 9.8%. Compared with the SCE-UA method, the optimized parameters obtained by NODE have higher simulation accuracy for the discharge process. The research shows that the parameter optimization method based on NODE can effectively search the parameter space through the forward solution of differential equations and the backpropagation of gradient information, which is suitable for the parameter optimization problem of the differential form hydrological model.
水文模型是洪水模拟预报的重要手段,结构和参数是水文模型的核心[1],其中参数用于描述流域下垫面特征,是保证模型精度的关键因素之一[2]。理论上,水文模型参数均可根据流域下垫面物理特征进行确定,但实际工作中通常需要采用实测水文资料,通过参数优化的方法来确定模型参数,以期达到模型模拟结果与观测数据之间的最佳匹配[3-4]。因此,提高参数优化性能对准确模拟流域水文过程具有重要意义。
目前参数优化中常用启发式算法,如遗传算法[5](genetic algorithm,GA)、粒子群算法[6](particle swarm optimization,PSO)和洗牌复形演化算法[7](shuffled complex evolution,SCE-UA)等,但这些算法也存在一定局限性,例如,GA算法由于交叉变异操作不足或种群规模较小等因素,在多目标优化时可能面临早熟收敛问题,进而难以得到全局最优解[6];PSO算法在处理复杂、多峰函数时容易陷入局部最优解[8],且对算法参数(如惯性权重、加速常数)的选择较为敏感[9];SCE-UA算法需要对多个复合形进行并行演化和交互,因算法的内在随机性,其参数优化结果可能不唯一[5],这些都增加了水文模型参数全局稳定最优解的难度。此外,近些年来流域水文模型理论也在不断完善,其中,为降低模型求解数值误差,水文模型的数学描述逐渐由差分形式向微分形式发展[10-11],因此微分形式水文模型参数优化是值得探讨的问题[12]。已有研究表明,深度学习模型能够捕捉水文模型的非线性关系[13-14],提供准确的参数估计[15],同时可更好地与微分方程表达的水文过程耦合[16-18],为水文模型参数优化提供了新的思路。Tsai等[19]提出一种可微参数学习框架,通过深度神经网络和自动微分技术,显著提升了模型参数优化的效率和性能。Feng等[20]将深度学习与水文模型结合,利用深度学习的泛化能力优化水文模型参数,在保证水文模型的模拟精度的同时,也提升了深度学习的可解释性。Höge等[16]提出了一种基于神经常微分方程的水文模型,采用神经网络替代集总式水文模型中的部分模块,将深度学习与水文物理机制进行了有效结合。
本文以微分形式新安江模型为例,将神经网络嵌入到水文模型结构中,每个模型参数建立一个神经网络,对包含神经网络的微分方程进行正向数值求解并反向传播梯度信息,通过训练得到的神经网络将流域下垫面属性映射为水文模型参数,从而形成基于神经常微分方程的水文模型参数优化方法,以提高水文模型模拟精度。
1 研究方法
1.1 神经常微分方程
常用的神经网络模型(如循环神经网络、长短期记忆网络等),通过离散时间序列上的递归连接,捕捉数据之间的隐含关系,对时间连续水文过程的描述存在一定的局限性。常微分方程适合刻画在时间上连续变化的物理过程,而神经常微分方程(neural ordinary differential equations,NODE)[21-22]通过耦合深度学习与常微分方程,使用神经网络近似物理状态随时间演化的连续函数,从而可更好地学习得到水文数据中隐含的非线性关系。在NODE中,时间连续变化过程可表示为[21]:
(1)
式中,h(t)为时间t的物理状态;θ为神经网络参数;f[·]为以神经网络表示的连续函数。
如图1所示,当使用有限采样的离散时间序列数据(如水文气象数据)构建NODE时,设定神经网络和状态初值h(0),根据公式(1)使用常微分方程求解器(如Runge Kutta法等)进行连续计算;在深度学习框架下,通过损失函数和对网络参数的梯度来调整神经网络权重,直至损失函数达到最小值且趋于稳定,进而得到预测轨迹。NODE可得到任意时间的预测值,所以更具灵活性;同时,NODE理论上可与微分形式的水文模型无缝耦合,在解决此类模型参数估计问题时更具优势。
1.2 微分形式新安江水文模型
微分形式的新安江模型(ordinary differential-form Xin'anjiang model,ODE-XAJ)以新安江模型原理与框架为基础,通过微分方程描述状态变量与通量之间的关系,可实现水文过程由离散时段(Δt)变为连续时间(dt)的表达[23-24]。ODE-XAJ的结构、参数含义及取值范围与现有三水源新安江模型[25]相同,其状态变量的微分控制方程组见公式(2),通量方程组参见文献[24],模型参数见表1。
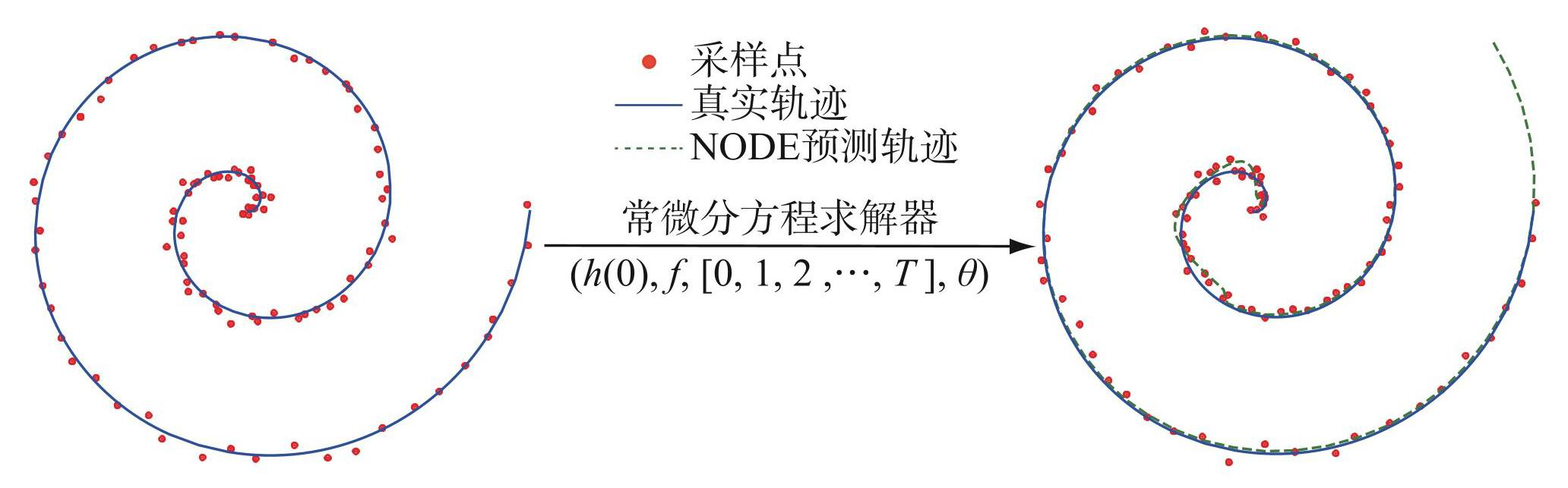
图1NODE时间序列拟合示意
Fig.1The time series fitting schematic diagram of NODE
(2)
式中,Wu、Wl和Wd分别为上层、下层、深层土壤张力水蓄量,mm;Pn为净雨强度,mm/d;R为产流强度,mm/d;Eu、El和Ed分别为上层、下层、深层土壤蒸散发强度,mm/d;Iu和Il分别为上层土壤向下层土壤补给强度和下层土壤向深层土壤补给强度,mm/d;Rs、Ri和Rg分别为地表径流、壤中流和地下径流强度,mm/d;Aimp为不透水面积比例;fw为全流域蓄满比例;S0为流域平均自由水蓄水量,mm;Oi和Og分别为壤中流/地下径流坡面汇流线性水库蓄水量,mm;Qi和Qg分别为壤中流/地下径流坡面汇流线性水库出流强度,mm/d;Qt为河网入流强度,mm/d;F1、F2和F3分别为Nash单位线子模块中3个水库的蓄水量,mm;Q1、Q2和Q3分别代表Nash单位线子模块中3个水库的出流强度,mm/d。
表1ODE-XAJ模型参数物理意义及取值范围
Tab.1 Physical meaning and value range of ODE-XAJ model parameters

1.3 基于NODE的微分形式新安江模型参数优化方法
基于NODE的水文模型参数优化方法如图2所示,其主要步骤包括:
(1)定义多层感知器[26](multilayer perceptron,MLP)神经网络,用于学习水文模型参数与流域属性数据之间的关系,其输出为0~1范围的值,再通过公式(3)将其转换成水文模型参数;
(2)将模型参数代入模型微分方程中,根据状态变量初始值和水文气象实测数据,使用常微分方程求解器进行正向数值求解,从而模拟水文过程;
(3)基于模拟及实测的流量过程,按照公式(4)计算损失函数;使用损失相对于神经网络参数的梯度(公式(5)),通过反向传播更新神经网络参数,进而得到新的水文模型参数值;
(4)重复步骤(2)和(3),直至损失函数值收敛,即可得到最优的水文模型参数估计值。
(3)
(4)
(5)
式中,δ为新安江模型的任一参数,δmax为其上限值,δmin为其下限值;σ(x)为sigmoid激活函数,其值域为(0,1);x为隐含层传递到输出层的激活值,其取值范围为实数域;L为损失函数,此处计算的是模拟流量和实测流量的均方误差;Qi为长度为n的序列中的第i个流量实测值,m3/s;为第i个流量模拟值,m3/s;θ为MLP神经网络参数。
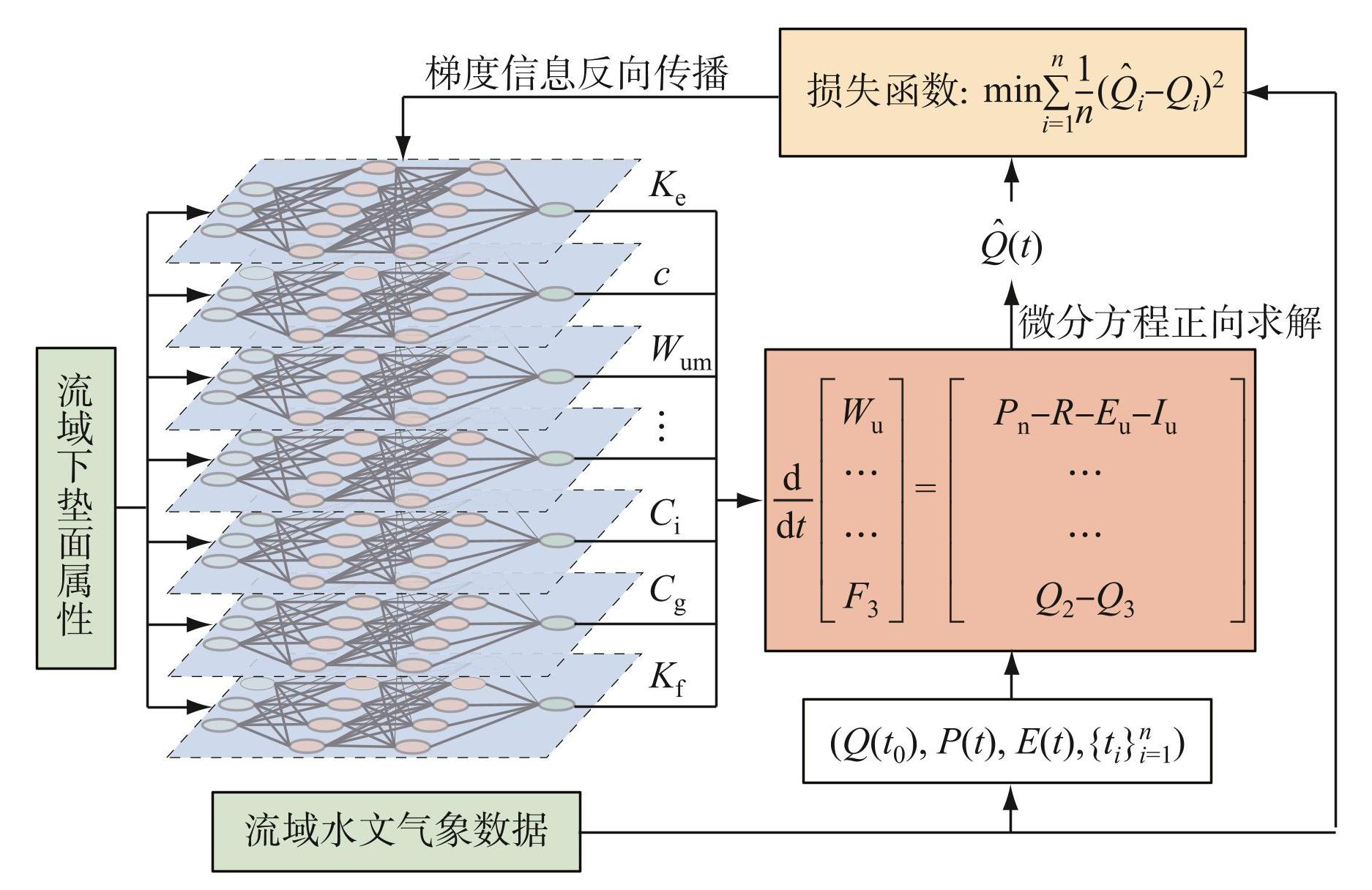
图2基于NODE的水文模型参数优化示意
Fig.2The diagram of hydrological model parameter optimization based on NODE
2 实验验证方案
为探究基于NODE的水文模型参数优化方法(以下简称NODE法)性能,设计了理想数值实验和典型流域应用两组验证方案,并与经典的SCE-UA法[7]进行对比。其中,理想数值实验用于验证NODE法是否能逼近设定的理想模型参数,典型流域示例用于检验该方法的实际应用精度。
考虑到MLP神经网络的输入为流域静态属性,使用简单的神经网络结构即可有效描述并取得良好的拟合效果[20,27],所以两组实验的MLP神经网络均设置2个隐含层,每个隐含层包含5个神经元。激活函数选择收敛速度较快的tanh函数,学习率设置为1×10-3,优化器使用Adam算法,迭代次数epoch设置为100次;常微分方程求解器使用基于Bogacki-Shampine的三阶Runge Kutta法[10],数值求解的相对容差和绝对容差均设为1×10-4。使用SCE-UA法率定水文模型参数时,搜索次数取2000,为避免寻优结果的随机性[28],重复10次率参过程,取其中效果最好的一组参数。
2.1 研究区及数据
选用皖南山区的屯溪流域作为研究区。屯溪流域位于新安江上游,属于湿润区流域,流域面积为2670 km2。流域地处亚热带季风气候区,雨量丰沛,多年平均降水约为1880 mm,降水年内分配不均且主要集中在6—9月的汛期,汛期降水占年内总降水的60%以上。流域位置、水系及站点分布如图3所示。
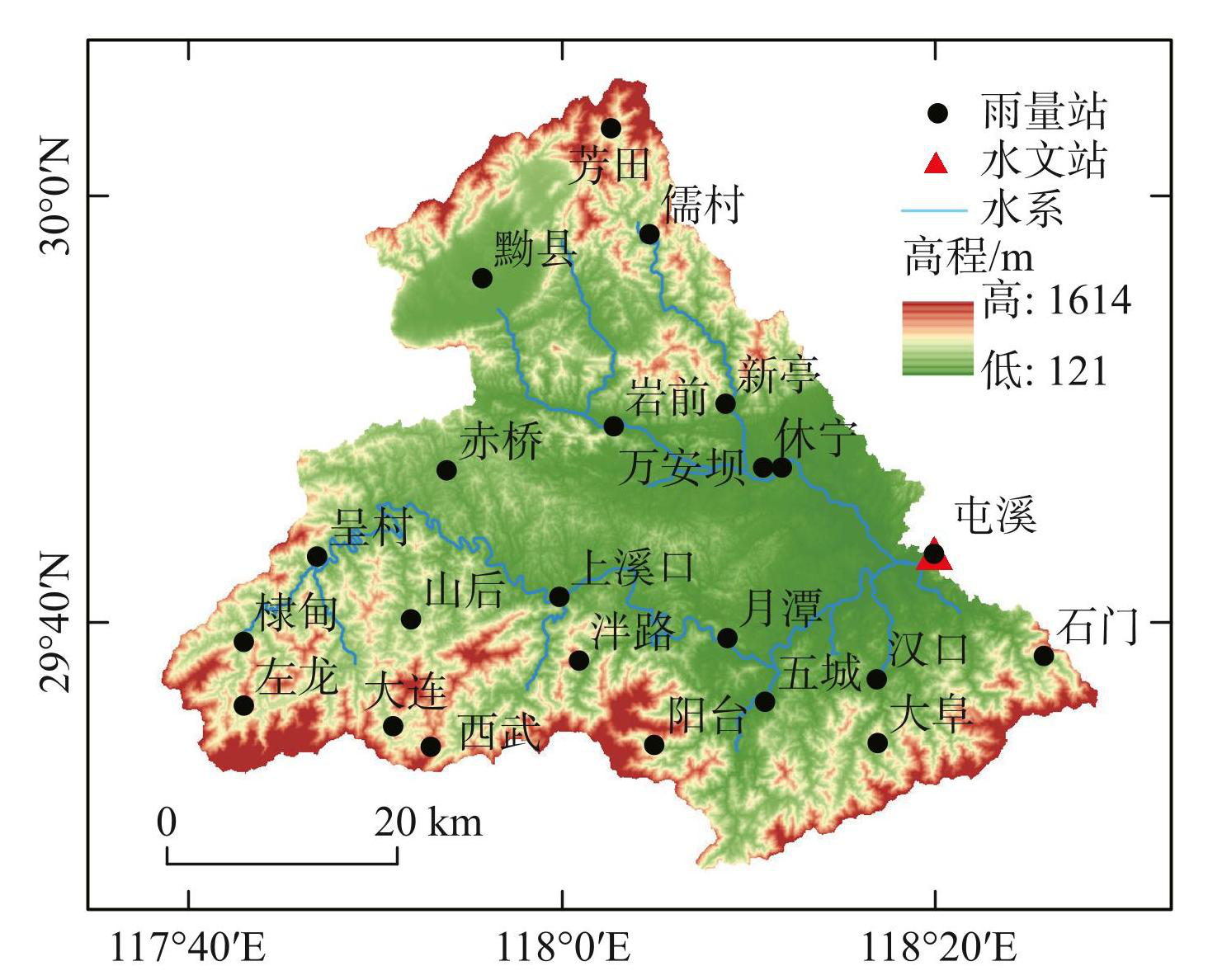
图3屯溪流域位置及站点分布
Fig.3Location and stations distribution of Tunxi watershed
使用屯溪流域的日尺度水文气象资料,包含屯溪水文站的逐日流量、日尺度蒸发数据、23个雨量站的逐日降水数据,流域面平均降水使用算术平均法计算。数据来源为《中华人民共和国水文年鉴》和中国地面气候资料日值数据集(V3.0),资料年限为2007—2019年。利用MLP神经网络学习新安江模型参数与流域属性之间的关系,依据模型参数物理意义选择流域属性[29-30],包括植被覆盖、土壤类型、流域面积、流域平均高程、流域最长汇流路径及比降等,具体见表2。
表2流域属性及其数据来源
Tab.2 Watershed attributes and data sources

2.2 理想数值实验
理想数值实验是人为假设一套水文模型参数作为参数的“真值”,再以实测或假定的降水、蒸发等数据作为模型输入,得到对应的水文模型输出,组成理想的输入-输出样本数据;依据理想样本数据,采用不同的参数优化方法得到模型参数的估计值;将估计的参数值与“真值”进行对比,以此评判不同优化方法的有效性。本文在假设水文模型参数“真值”时,基于屯溪流域2007—2019年(13年)的降水、蒸发及流量数据,率定了一套模型参数,然后将其作为“真值”参数。为节约计算时间并验证方法的泛化能力,在13年资料中选取了2007年1月1日-2010年7月23日(时期1)和2016年6月10日-2019年12月31日(时期2)两个时期(每个时期均为1300天)的降水和蒸发数据作为新安江模型的输入,采用“真值”参数,分别生成两个时期对应的1300天理想流量序列;再依据理想流量序列,分别采用SCE-UA和NODE法率定模型参数,其中第1~700天为率定期(深度学习的训练集),第701~1300天为验证期(深度学习的验证集和测试集)。并将两种方法的优化参数与“真值”参数进行对比,依据其与“真值”的接近程度来评估两种方法对水文模型参数的优化性能。
采用均方误差(mean square error,EMS)作为损失函数,判断训练收敛情况[31];选用相对误差(relative error,RE)指标,衡量优化的模型参数与“真值”之间的接近程度;使用平均绝对误差[31](mean absolute error,EMA)和纳什效率系数[32](Nash-Sutcliffe efficiency,ENS)评估流量模拟效果。RE计算公式为:
(6)
式中,RE为估计参数与参数“真值”之间的相对误差;δ为参数“真值”; 为参数估计值。
2.3 典型流域应用
根据屯溪流域实测水文气象数据,使用两种参数优化方法分别率定ODE-XAJ模型参数,并统计模型的模拟精度。其中,2007—2013年为率定期(深度学习的训练集),2014—2019年为验证期(深度学习的验证集和测试集)。用ENS、Kling-Gupta效率系数EKG[33]以及洪量相对误差(flood volume relative error,EFVR)对流量模拟结果进行评价,以分析两种参数优化方法的性能。EFVR公式为:
(7)
式中,EFVR为实测洪量与模拟洪量之间的洪量相对误差;V为实测洪量,m3;为模拟洪量,m3。
3 结果与讨论
3.1 理想数值实验结果
3.1.1 NODE法训练收敛情况
利用两种优化方法在理想数据的率定期分别进行参数优化,NODE法训练过程中损失函数随迭代次数的变化如图4所示。从图4中可看出,在训练的初始阶段,两个时期的EMS均较大;随着迭代次数的增加,两个时期的EMS均开始快速减小,表明新安江模型参数在训练过程得到有效优化;迭代次数超过50次后,EMS均逐渐趋于平稳;在迭代次数为90时,两个时期的EMS值分别为0.16和0.11,并且进一步增加迭代次数,EMS基本不再下降,表明训练达到收敛状态。
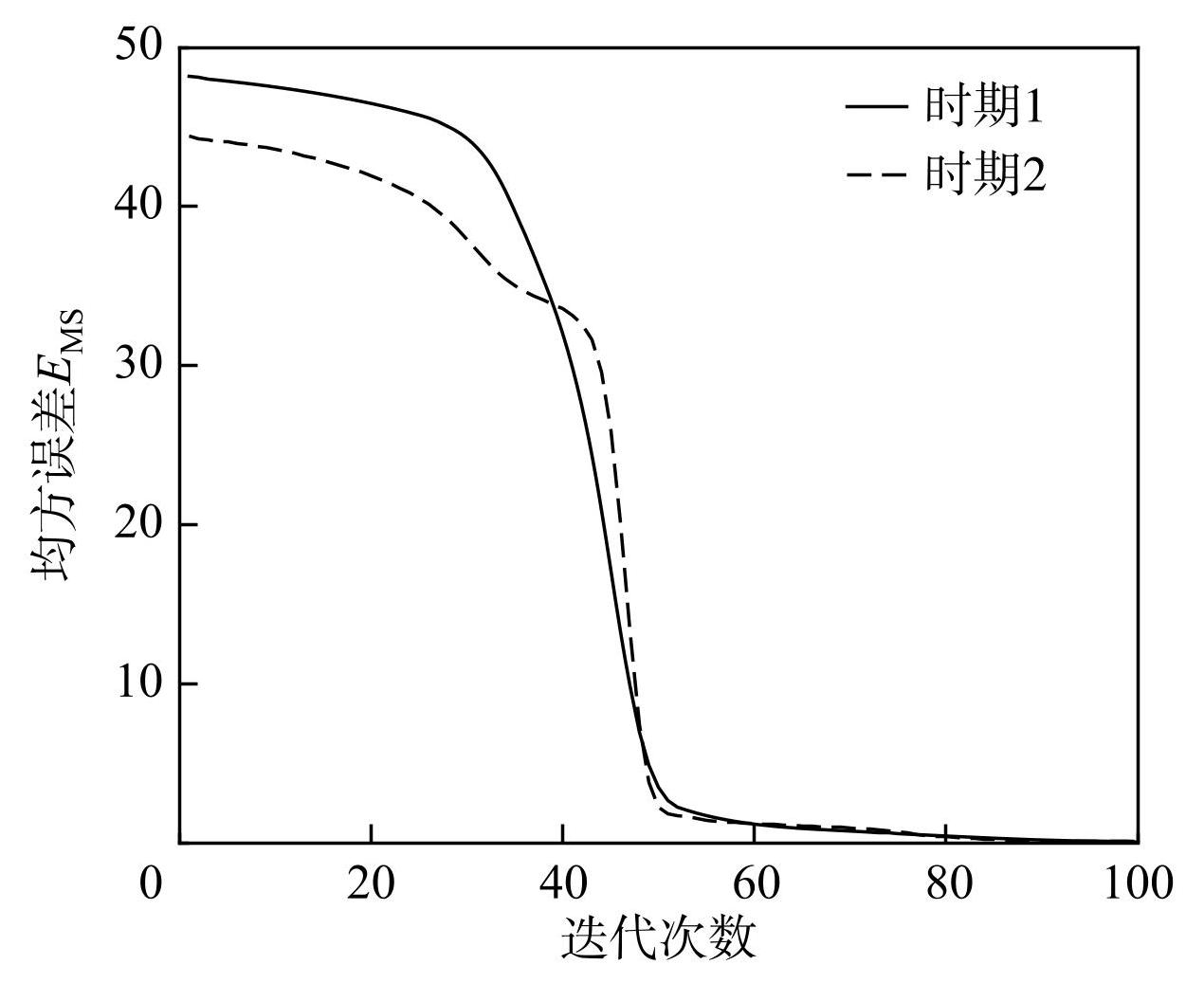
图4理想数值实验损失函数变化情况
Fig.4Variation of loss function for ideal numerical experiments
3.1.2 理想数值实验参数优化结果
理想数值实验中,利用两种优化方法分别率定参数,并比较两种优化方法对应的估计参数与参数“真值”之间的误差。由表3可知,在时期1中,SCE-UA法对应RE的绝对值平均为28.5%,最大值为186.3%;NODE法对应RE的绝对值平均为9.8%,最大值为52.9%。在时期2中,SCE-UA法RE的绝对值平均为27.0%,最大值为182.4%;NODE法参数优化的RE绝对值平均为7.5%,最大值为17.7%。从RE的绝对值平均和最大值来看,NODE法均小于SCE-UA法。针对新安江模型的敏感参数Ke、c、b、Sm、Ki、Kg、Ci以及Cg[30],NODE法对应RE绝对值整体小于SCE-UA方法。由此可知,相比于SCE-UA法,NODE法的参数结果更接近参数“真值”。
3.1.3 理想数值实验验证期流量模拟结果
表4为两组理想数值实验的模拟流量结果精度统计。整体而言,根据两种优化方法确定后的模型参数,均能较好地模拟理想流量序列,相较而言,NODE法对应模拟结果的EMA和ENS均优于SCE-UA法。作为示例,图5给出了时期1的验证期模拟流量过程,发现两种方法均能有效拟合流量的变化过程,但从局部来看(图5b、c),SCE-UA法对应模拟流量过程在洪峰以及退水段与理想序列存在一定偏差,而NODE法可有效克服这一现象。
表3理想数值实验参数优化结果
Tab.3 Parameter optimization results in ideal numerical experiments
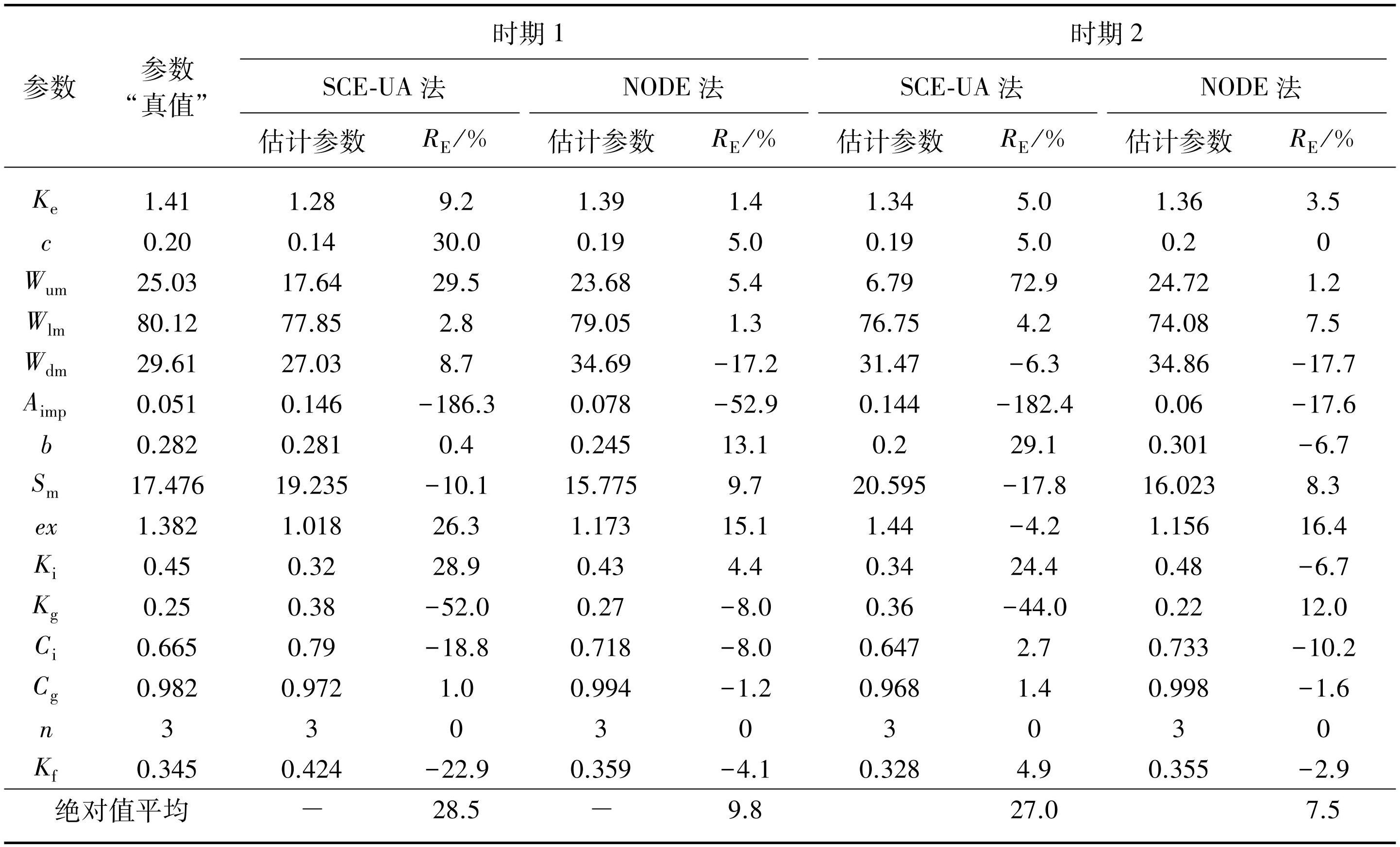
表4理想数值实验模拟流量结果精度统计
Tab.4 Accuracy statistics of simulated discharge results in ideal numerical experiments

上述结果表明,在相同的理想样本序列下,NODE法通过连续动态路径搜索参数空间,更准确地逼近参数“真值”,具有更优的模拟预测性能。
此外,对于两种方法的优化耗时,在相同CPU硬件条件和精度水平(ENS=0.98)下,SCE-UA法的耗时为1560s,NODE法为2091s。
3.2 典型流域应用结果
典型流域应用中,使用两种优化方法分别率定参数并进行流量模拟。由表5可知,SCE-UA法和NODE法在屯溪流域应用中均具有较高的模拟精度。对比SCE-UA法,NODE法模拟结果在率定期的ENS均值增加0.03、EKG均值提升0.02、EFVR的绝对均值降低2.69%,NODE法模拟结果在验证期的ENS和EKG均值都增加0.02、EFVR绝对均值降低4.52%。
以屯溪流域2018年实测与模拟的流量过程为例,其“实测流量-模拟流量”散点如图6所示。根据模拟和实测流量过程计算评价指标,用以分析两种优化方法的优劣。其中,NODE法和SCE-UA法对应的相关系数[13]分别为0.90和0.88,NODE法对应的散点更接近1∶1线。图7给出了屯溪流域2018年实测与两种优化方法对应的模拟流量过程线。如图所示,SCE-UA法和NODE法对应模拟流量过程均有较高的精度,但从局部大洪水(图7b)、小洪水过程(图7c)来看,NODE法的模拟结果与实测值更接近,表现出较好的稳定性和准确性。屯溪流域应用结果表明,针对微分形式新安江模型,NODE法具有更好的参数优化性能。
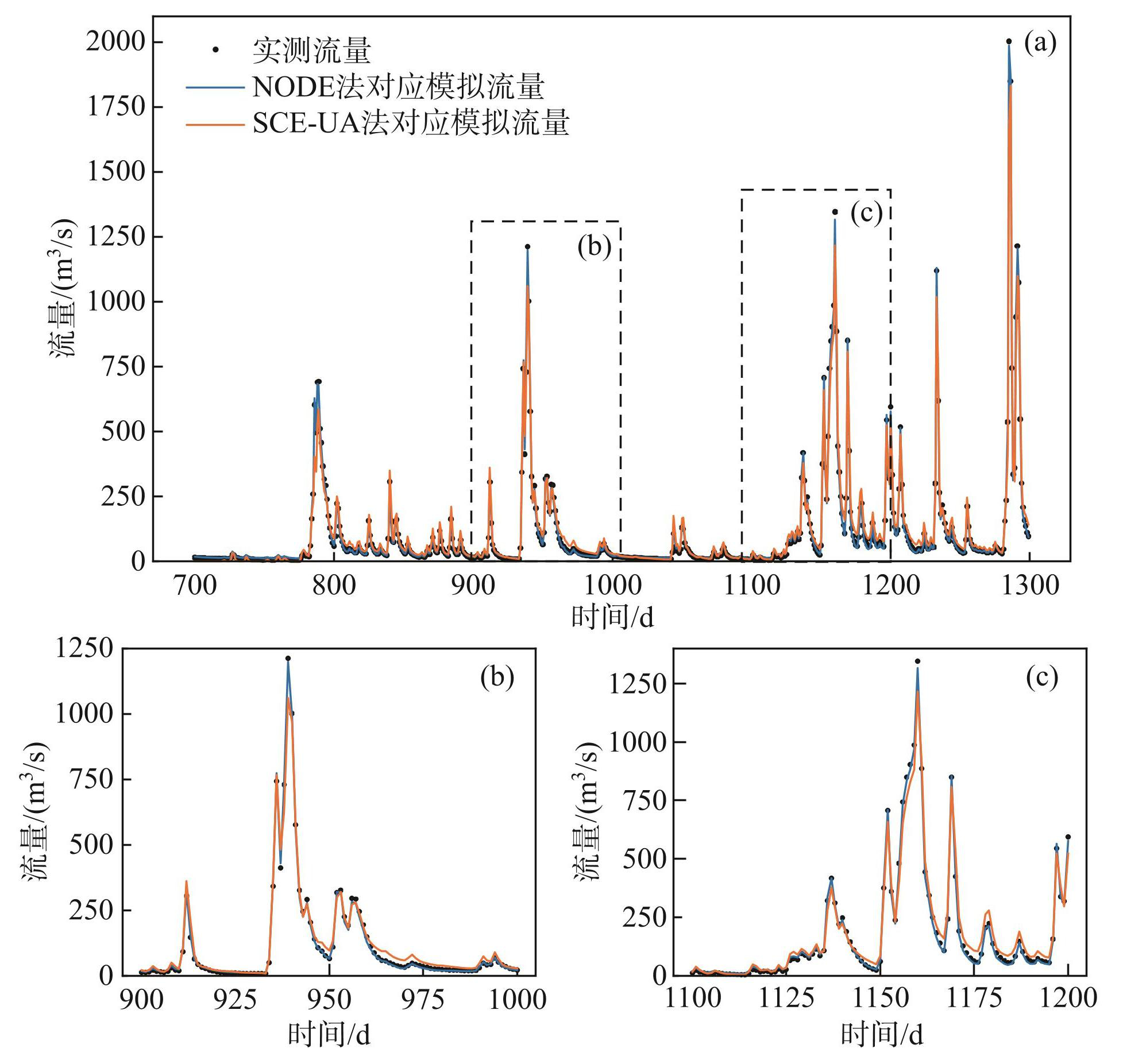
图5理想数值实验时期1实测与模拟流量过程对比(验证期)
Fig.5The comparison between the observed and simulated hydrograph in the first period of ideal numerical experiment (verification period)
表5屯溪流域模拟流量精度统计
Tab.5 Accuracy statistics of simulated discharge in Tunxi watershed
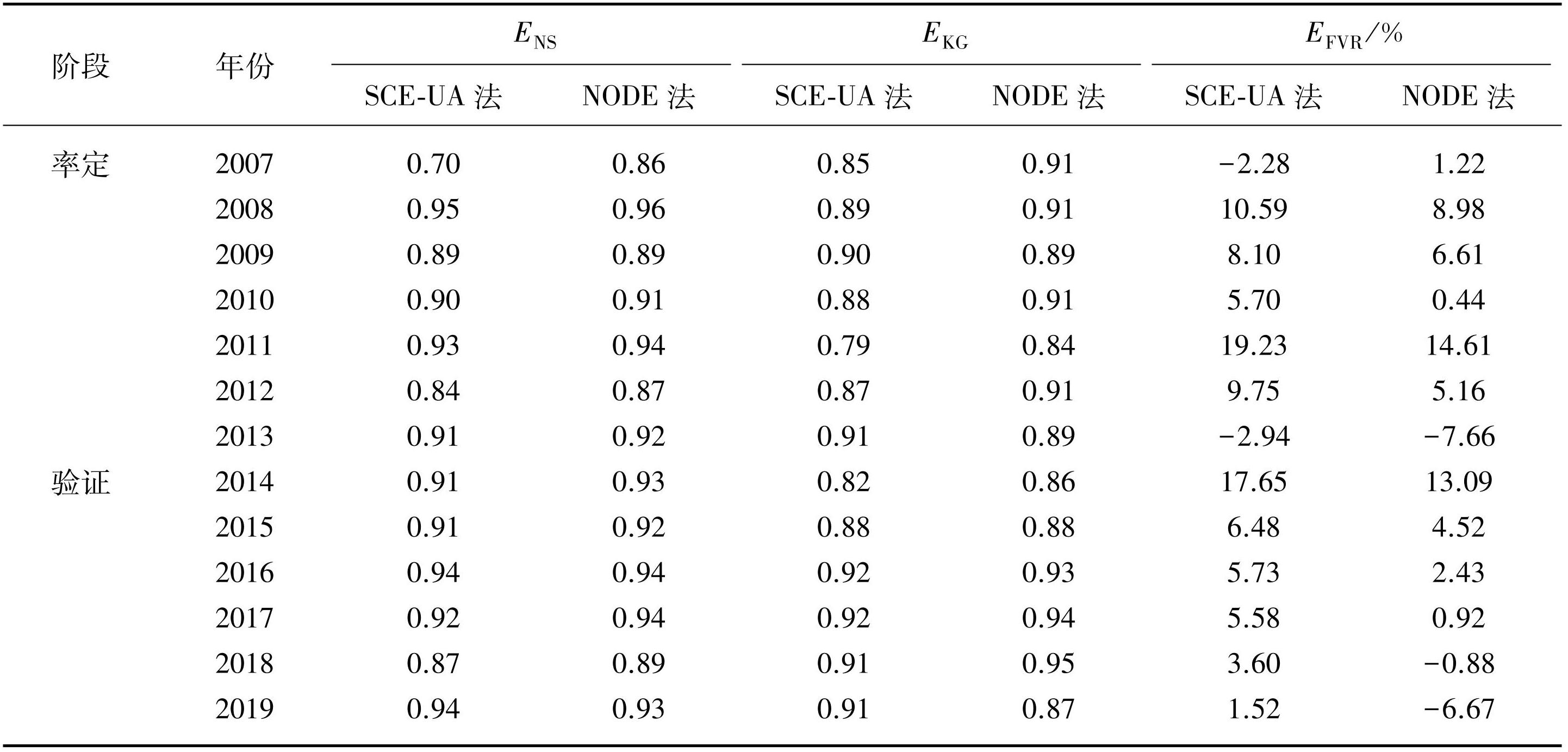
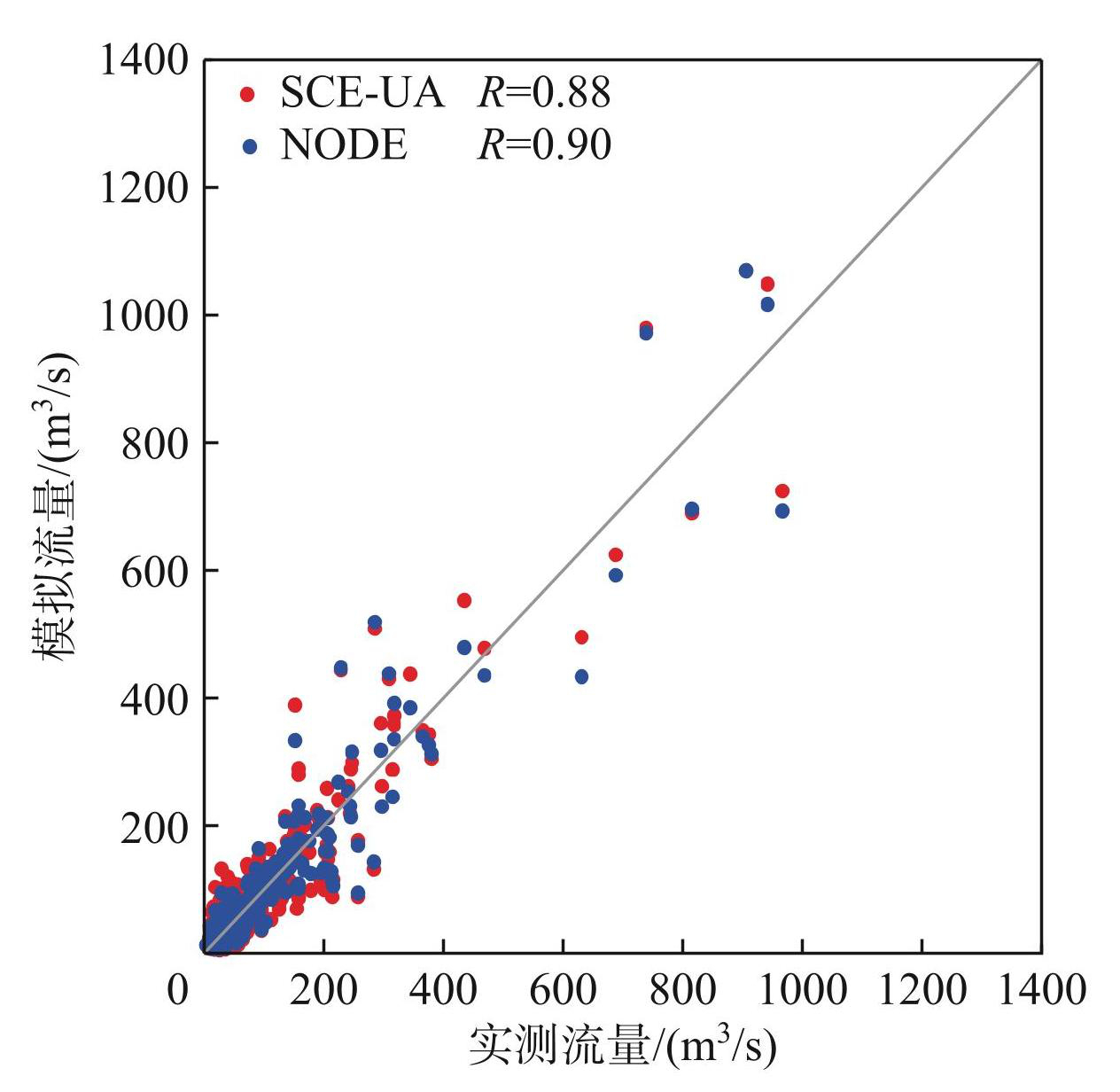
图6屯溪流域2018年实测流量与模拟流量散点图
Fig.6The scatter of observed discharge and simulated discharge of Tunxi watershed in 2018

图7屯溪流域2018年实测流量与模拟流量过程对比
Fig.7Comparison of the observed and simulated hydrograph of Tunxi watershed in 2018
4 结论
本文构建了基于神经常微分方程(NODE)的水文模型参数优化方法,并以新安江模型为例,设计了理想数值实验和典型流域应用两种方案进行验证研究,主要结论如下:
1)NODE能够充分利用水文模型的物理机制和深度学习的数据挖掘能力,可解决微分形式水文模型的参数优化问题,通过较少的迭代次数可以得到水文模型最优参数。
2)与目前常用的SCE-UA优化方法相比,NODE参数优化方法可以得到更优的水文模型参数估计值;屯溪流域的初步应用结果表明,相同的输入数据条件下,根据NODE确定的模型参数具有更高的模拟精度。
3)尽管NODE法在水文模型参数优化中显示出一定优势,但其普适性仍有待更多的检验,未来将结合不同气候区(如半湿润半干旱区)和下垫面条件的实际流域对该方法进行应用验证。
